
附加题:若将题中“直线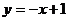 ”改为“直线
”改为“直线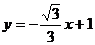 ”、“含45º角的直角三角板的锐角顶点A在线段CD上滑动”改为“含30º角的直角三角板的30º角的顶点A在线段CD上滑动”(如图),其他条件不变,试探索△AOB能否为等腰三角形。若能,请求出点B的坐标;若不能,请说明理由。
”、“含45º角的直角三角板的锐角顶点A在线段CD上滑动”改为“含30º角的直角三角板的30º角的顶点A在线段CD上滑动”(如图),其他条件不变,试探索△AOB能否为等腰三角形。若能,请求出点B的坐标;若不能,请说明理由。
(2)若将题中“直线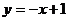 ”、“∠A的另一边与
”、“∠A的另一边与 轴的正半轴相交于点B”分别改为“直线
轴的正半轴相交于点B”分别改为“直线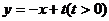 ”、“∠A的另一边与
”、“∠A的另一边与 轴的负半轴相交于点B”(如图2),其他条件不变,试探索△AOB能否为等腰三角形(只考虑点A在线段CD的延长线上且不包括点D时的情况)。若能,请求出点B的坐标;若不能,请说明理由
轴的负半轴相交于点B”(如图2),其他条件不变,试探索△AOB能否为等腰三角形(只考虑点A在线段CD的延长线上且不包括点D时的情况)。若能,请求出点B的坐标;若不能,请说明理由
26.如图1,直线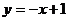 与
与 轴、
轴、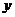 轴分别相交于点C、D,一个含45º角的直角三角板的锐角顶点A在线段CD上滑动,滑动过程中三角板的斜边始终经过坐标原点,∠A的另一边与
轴分别相交于点C、D,一个含45º角的直角三角板的锐角顶点A在线段CD上滑动,滑动过程中三角板的斜边始终经过坐标原点,∠A的另一边与 轴的正半轴相交于点B。
轴的正半轴相交于点B。
(1)试探索△AOB能否构成以AO、AB为腰的等腰三角形。若能,请求出点B的坐标;若不能,说说明理由;
25.如图1,点D、F、A、E在同一直线上,且AE=DF,分别以DA、AE为一边,在直线DE的同侧作等边△DBA和等边△ACE,试证明△BCF也是等边三角形。
(1)下面是小伟对此题的分析过程,请你根据他的分析填空:此题中,要想证明△BCF是等边三角形,至少要证明两条边相等。欲证两条边相等,可以通过证明这两条边所在的两个三角形全等来实现。根据已知条件,在不加辅助线的情况下,不妨尝试证明 ≌△ABC,依据是 (写出定义、公理或定理的内容);
(2)如图2,点D、B、C在同一直线上,分别以DB、BC为一边,在直线DC的同侧作等边△DBA和等边△BCF,再以DA、DF为邻边作□ADFE,求证:△ACE是等边三角形;
(3)图3是将(2)中的等边△BCF绕点B顺时针旋转一个角度后得到的图形,若其他条件不变,△ACE是否还是等边三角形?请加以说明。
(3)如果将(2)中的“同侧”改为“异侧”(如图2),其他条件不变,并设M为直线 与
与 轴交点,
轴交点,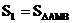 ,
,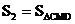 ,求
,求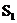 、
、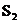 与
与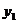 、
、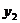 的数量关系(直接写出答案)。
的数量关系(直接写出答案)。
(2)当抛物线 在
在 轴上方,且点
轴上方,且点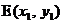 、
、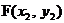 在抛物线
在抛物线 的对称轴的同侧(点E在点F的左侧)时(如图1),(1)中的结论是否仍然成立?请说明你的判断;
的对称轴的同侧(点E在点F的左侧)时(如图1),(1)中的结论是否仍然成立?请说明你的判断;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com