
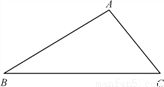
已知:如图,在△ABC中,∠B=30°,∠C=45°,AC=2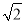 ,求S△ABC.
,求S△ABC.
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:初中数学 来源:2017年广东省韶关市南雄市中考数学模拟试卷 题型:填空题
已知2x2+3x+1的值是10,则代数式x2+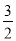 x﹣2的值是_____.
x﹣2的值是_____.
查看答案和解析>>
科目:初中数学 来源:山东省德州市2017-2018学年九年级上学期期中考试数学试卷 题型:解答题
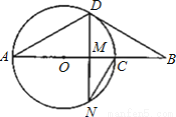
如图,线段AB经过圆心O,交⊙O于A、C两点,点D在⊙O上,∠A=∠B=30°.
(1)求证:BD是⊙O的切线;
(2)若点N在⊙O上,且DN⊥AB,垂足为M,NC=10,求AD的长.
查看答案和解析>>
科目:初中数学 来源:山东省德州市2017-2018学年九年级上学期期中考试数学试卷 题型:单选题
在平面直角坐标系xOy中,抛物线y=2x2+mx+8的顶点在x 轴负半轴上,则m的值是( )
A. ±4 B. 8 C. -8 D. ±8
B 【解析】试题分析:∵抛物线y=2x2+mx+8的顶点A在x 轴上, ∴. 又∵点A在y轴左侧, ∴. 故选B.查看答案和解析>>
科目:初中数学 来源:2018年春人教版八年级数学下册(广西)期末测试 题型:解答题
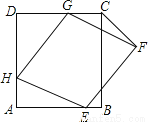
如图,菱形EFGH的三个顶点E、G、H分别在正方形ABCD的边AB、CD、DA上,连接CF.
(1)求证:∠HEA=∠CGF;
(2)当AH=DG时,求证:菱形EFGH为正方形.
查看答案和解析>>
科目:初中数学 来源:2018年春人教版八年级数学下册(广西)期末测试 题型:填空题
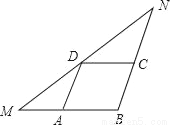
如图,在△MBN中,已知:BM=6,BN=7,MN=10,点A,C,D分别是MB,NB,MN的中点,则四边形ABCD的周长是_____.
查看答案和解析>>
科目:初中数学 来源:2018年春人教版八年级数学下册(广西)期末测试 题型:单选题
若实数a,b满足ab<0,则一次函数y=ax+b的图象可能是( )
A. 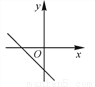 B.
B. 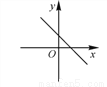 C.
C. 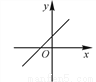 D.
D. 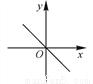
查看答案和解析>>
科目:初中数学 来源:江西省2017-2018学年度八年级第三次月考数学试卷 题型:填空题
如图,已知BD,CD分别是 ∠ABC和∠ACE的平分线,连接AD,∠DAC=46°, ∠BDC _________
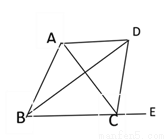
查看答案和解析>>
科目:初中数学 来源:山西省2017-2018学年八年级上期末模拟数学试卷 题型:解答题
如图,∠MON=30°,在距离O点80米的A处有一所学校,当重型运输卡车P沿道路ON方向行驶时,距离卡车50米范围内都会受到卡车噪声的影响.
(1)学校A是否受到卡车噪声的影响?为什么?
(2)假如学校A会受到噪声的影响,若卡车以每小时18km的速度行驶,求卡车P沿道路ON方向行驶一次给学校A带来噪声影响的时间.
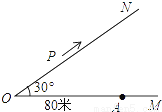
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com