
一元二次方程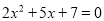 根的情况是 ( )
根的情况是 ( )
A. 有不等实根 B. 有相等实根 C. 无实根 D. 无法确定
C 【解析】先计算判别式的值,然后根据判别式的意义判断根的情况. 【解析】 ∵△=52?4×7=?3<0, ∴方程没有实数根. 故选C. 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2017年吉林省中考数学一诊试卷 题型:单选题
如图是由几个大小相同的小正方体搭成的几何体的俯视图,小正方形中数字表示该位置小正方体的个数,则该几何体的左视图是( )
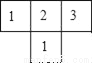
A.  B.
B. 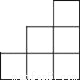 C.
C.  D.
D. 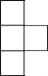
查看答案和解析>>
科目:初中数学 来源:2017年吉林省长春市中考数学模拟试卷(7) 题型:填空题
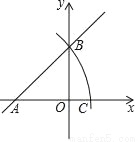
如图,在平面直角坐标系中,直线y=x+b交x轴于点A,交y轴于点B,以点A为圆心,线段AB长为半径作圆弧,交x轴正半轴于点C,若AC=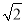 ,则b的值为_____.
,则b的值为_____.
查看答案和解析>>
科目:初中数学 来源:山东省2018届九年级12月月考数学试卷 题型:解答题
若方程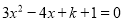 无实数根,化简:
无实数根,化简: 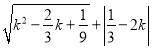
查看答案和解析>>
科目:初中数学 来源:山东省2018届九年级12月月考数学试卷 题型:填空题
如图,AB是⊙O的直径,AC是⊙O的切线,A为切点,连接BC交⊙O于点D,若∠C=50°,则∠AOD=__°.
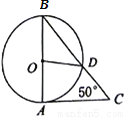
查看答案和解析>>
科目:初中数学 来源:山东省2018届九年级12月月考数学试卷 题型:单选题
用配方法解一元二次方程ax2+bx+c=0(a≠0),此方程可变形为( )
A. 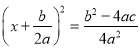 B.
B. 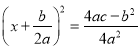
C. 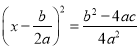 D.
D. 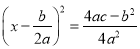
查看答案和解析>>
科目:初中数学 来源:湖北省武汉市汉阳区2018届九年级(上)期中数学试卷(解析版) 题型:解答题
关于x的一元二次方程x2+(2k+1)x+k2+1=0有两个不等实根x1,x2.
(1)求实数k的取值范围;
(2)若方程两实根x1,x2满足|x1|+|x2|=x1·x2,求k的值.
(1) k>;(2)k=2 【解析】试题分析:(1)根据根与系数的关系得出△>0,代入求出即可; (2)根据根与系数的关系得出x1+x2=﹣(2k+1),x1•x2=k2+1,根据x1+x2=﹣x1•x2得出﹣(2k+1)=﹣(k2+1),求出方程的解,再根据(1)的范围确定即可. 试题解析:(1)∵原方程有两个不相等的实数根, ∴△=(2k+1)2﹣4(k2+1)>0, ...查看答案和解析>>
科目:初中数学 来源:湖北省武汉市汉阳区2018届九年级(上)期中数学试卷(解析版) 题型:单选题
将一元二次方程3x2+1=6x化为一般形式后,常数项为1,二次项系数和一次项系数分别为( )
A. 3,﹣6 B. 3,6 C. 3,1 D. 3x2,﹣6x
A 【解析】由题意得3x2-6x+1=0, 二次项系数是3,一次项系数是-6,故选A.查看答案和解析>>
科目:初中数学 来源:2017年海南省海口市中考数学模拟试卷 题型:单选题
已知⊙O的半径为6,A为线段PO的中点,当OP=10时,点A与⊙O的位置关系为( )
A. 在圆上 B. 在圆外 C. 在圆内 D. 不确定
C 【解析】试题解析:∵OP=10,A是线段OP的中点, ∴OA=5,小于圆的半径6, ∴点A在圆内. 故选C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com