
用配方法解一元二次方程ax2+bx+c=0(a≠0),此方程可变形为( )
A. 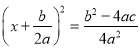 B.
B. 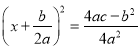
C. 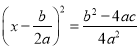 D.
D. 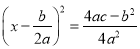
科目:初中数学 来源:2017年贵州省中考数学二模试卷 题型:解答题
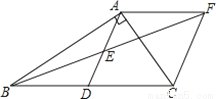
在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=3,AB=4,求菱形ADCF的面积.
查看答案和解析>>
科目:初中数学 来源:2017年吉林省长春市中考数学模拟试卷(7) 题型:单选题
如图,A,B,C为⊙O上三点,若∠ACB=20°,则∠BAO的大小为( )
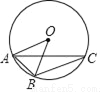
A. 40° B. 60° C. 70° D. 80°
C 【解析】∵∠ACB=20°, ∴∠AOB=2×20°=40°, ∵AO=BO, ∴∠BAO=∠OBA=(180°?40°)÷2=70°, 故选:C.查看答案和解析>>
科目:初中数学 来源:山东省2018届九年级12月月考数学试卷 题型:填空题
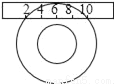
如图所示,一个宽为2cm的刻度尺在圆形光盘上移动,当刻度尺的一边与光盘相切时,另一边与光盘边缘两个交点处的读数恰好是“2”和“10”(单位:cm),那么该光盘的直径是_____cm.
查看答案和解析>>
科目:初中数学 来源:山东省2018届九年级12月月考数学试卷 题型:单选题
一元二次方程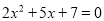 根的情况是 ( )
根的情况是 ( )
A. 有不等实根 B. 有相等实根 C. 无实根 D. 无法确定
C 【解析】先计算判别式的值,然后根据判别式的意义判断根的情况. 【解析】 ∵△=52?4×7=?3<0, ∴方程没有实数根. 故选C.查看答案和解析>>
科目:初中数学 来源:湖北省武汉市汉阳区2018届九年级(上)期中数学试卷(解析版) 题型:解答题
某商场销售一种产品,每件产品的成本为2400元,销售单价定位3000元,该商场为了促销,规定客户一次购买这种新型产品不超过10件时,每件按3000元销售;若一次购买该种产品超过10件时,每多购买一件,所购买的全部产品的销售单价均降低10元,但销售单价均不低于2600元;
(1)设一次购买这种产品x(x≥10)件,商场所获的利润为y元,求y(元)与x(件)之间的函数关系式,并写出自变量x的取值范围;
(2)在客户购买产品的件数尽可能少的前提下,商场所获的利润为12000元,此时该商场销售了多少件产品?
(3)填空:该商场的销售人员发现,当客户一次购买产品的件数在某一个区间时,会出现随着一次购买的数量的增多,商场所获的利润反而减少这一情况,客户一次购买产品的数量x满足的条件是 (其它销售条件不变)
(1);(2)30;(3)35<x≤50. 【解析】试题分析:(1)利用单价利润件数=利润列函数关系式,按照不同条件要列分段函数,注意求定义域.(2)令函数值为12000,解方程.(3)求二次函数的增减性, y随x的增大而减小. 试题解析: 【解析】 (1)当一次购买这种产品x(x≥10)件时,销售单价为3000﹣10(x﹣10),由题意可知,3000﹣10(x﹣10)≥260...查看答案和解析>>
科目:初中数学 来源:湖北省武汉市汉阳区2018届九年级(上)期中数学试卷(解析版) 题型:填空题
如图,用篱笆靠墙围成矩形花圃ABCD,墙可利用的最大长度为15m,一面利用旧墙,其余三面用篱笆围,篱笆长为24m,若围成的花圃面积为40m2时,平行于墙的BC边长为_____m.

查看答案和解析>>
科目:初中数学 来源:江苏省扬州市2016届九年级下学期二模数学试卷 题型:解答题
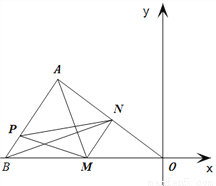
如图,在平面直角坐标系中,△AOB的三个顶点的坐标分别是A(-4,3),B(-6,0), O是原点.点M是OB边上异于O,B的一动点,过点M作MN//AB,点P是AB边上的任意点,连接AM,PM,PN,BN.设点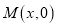 .
.
(1)求出OA所在直线的解析式,并求出点M的坐标为(-1,0)时,点N的坐标.
(2)若 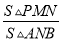 =
=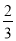 时,求此时点N的坐标.
时,求此时点N的坐标.
查看答案和解析>>
科目:初中数学 来源:2017年海南省海口市中考数学模拟试卷 题型:单选题
化简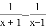 ,可得( )
,可得( )
A. 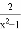 B.
B. 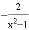 C.
C. 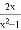 D.
D. 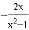
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com