
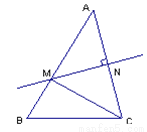
如图,在△ABC中,AB=8,BC=6,AC的垂直平分线MN交边AB、AC于点M、N.则△BCM的周长为_________.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:浙江杭州下城区安吉路实验学校2017-2018学年七年级上学期期中数学试卷 题型:填空题
若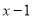 与
与 是同一个数的平方根,则
是同一个数的平方根,则 __________.
__________.
查看答案和解析>>
科目:初中数学 来源:浙江省温州市2017-2018学年浙教版8年级上数学期末练习 题型:解答题
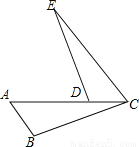
已知:如图,点A,D,C在同一直线上,AB∥EC,AC=CE,∠B=∠EDC,求证:BC=DE
查看答案和解析>>
科目:初中数学 来源:浙江省温州市2017-2018学年浙教版8年级上数学期末练习 题型:单选题
不等式5-2x>0的解集是( )
A. x<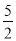 B. x>
B. x>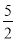 C. x<
C. x<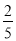 D. x<?
D. x<?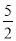
查看答案和解析>>
科目:初中数学 来源:新疆阿克苏十二中2017-2018学年八年级(上)期中数学试卷 题型:解答题
如图,△ABC中,∠A=50°,∠ABC的平分线与∠C的外角∠ACE平分线交于D,求∠D的度数.
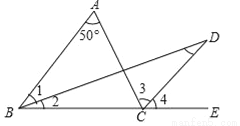
查看答案和解析>>
科目:初中数学 来源:新疆阿克苏十二中2017-2018学年八年级(上)期中数学试卷 题型:填空题
等腰三角形一个角为50°,则此等腰三角形顶角为 .
50°或80°. 【解析】 试题分析:已知没有给出50°的角是顶角和是底角,所以要分两种情况进行讨论. 【解析】 分为两种情况: 当50°是顶角时,顶角为50° 当50°是底角时,其顶角是180°﹣50°×2=80° 故填50°或80°.查看答案和解析>>
科目:初中数学 来源:新疆阿克苏十二中2017-2018学年八年级(上)期中数学试卷 题型:单选题
如图,在△ABC中,∠A=80°,∠B=40°,D,E分别是AB,AC上的点,且DE∥BC,则∠AED的度数为( )
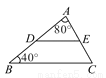
A. 40° B. 60° C. 80° D. 120°
B 【解析】试题分析:本题考查了三角形内角和定理、平行线的性质.解题时,要挖掘出隐含在题干中的已知条件:三角形的内角和是180°.根据两直线平行(DE∥BC),同位角相等(∠ADE=∠B)可以求得△ADE的内角∠ADE=40°;然后在△ADE中利用三角形内角和定理即可求得∠AED的度数.∵DE∥BC(已知),∠B=40°(已知),∴∠ADE=∠B=40°(两直线平行,同位角相等);又∵∠A=...查看答案和解析>>
科目:初中数学 来源:江苏省苏州市区2017-2018学年第一学期九年级数学期末考试试卷 题型:填空题
一圆锥的侧面积为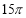 ,底面半径为3,则该圆锥的母线长为 .
,底面半径为3,则该圆锥的母线长为 .
查看答案和解析>>
科目:初中数学 来源:福建省泉州台商投资区2017-2018学年八年级上学期期末教学质量检测数学试卷 题型:解答题
如图,△ABC中,AC=BC=10 cm,AB=12 cm,点D是AB的中点,连结CD,动点P从点A出发,沿A→C→B的路径运动,到达点B时运动停止,速度为每秒2 cm,设运动时间为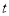 秒.
秒.
(1)求CD的长;
(2)当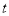 为何值时,△ADP是直角三角形?
为何值时,△ADP是直角三角形?
(3)直接写出:当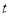 为何值时,△ADP是等腰三角形?
为何值时,△ADP是等腰三角形?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com