
如图所示,点D在△ABC的AB边上,AD=2,BD=4,AC= 2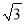 .
.
求证:△ACD∽△ABC.
科目:初中数学 来源:人教版九年级上册数学 第24章小结与复习 测试 题型:填空题
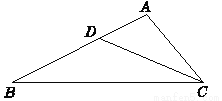
如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点.若⊙O的半径为7,则GE+FH的最大值为 .
查看答案和解析>>
科目:初中数学 来源:湖北省大冶市金湖街办2017-2018学年八年级上学期第二次月考(12月)数学试卷 题型:单选题
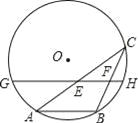
我国传统建筑中,窗框(如图①)的图案玲珑剔透、千变万化.窗框一部分如图②所示,它是一个轴对称图形,其对称轴有( )
A. 1条 B. 2条 C. C.3条 D. D.4条
B 【解析】【解析】 如图所示: 其对称轴有2条.故选B.查看答案和解析>>
科目:初中数学 来源:辽宁省2017-2018学年七年级上学期期末考试数学试卷 题型:单选题
如图,已知线段a、b(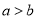 ),画一条线段AD,使它等于
),画一条线段AD,使它等于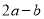 ,正确的画法是( )
,正确的画法是( )
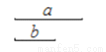
A. 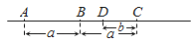 B.
B. 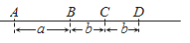
C. 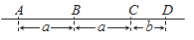 D.
D. 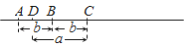
查看答案和解析>>
科目:初中数学 来源:浙江省湖州市吴兴区2017-2018学年九年级上学期期末考试数学试卷 题型:解答题
某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=1米;上部△CDG是等边三角形,固定点E为AB的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆.
(1)当MN和AB之间的距离为0.5米时,求此时△EMN的面积;
(2)设MN与AB之间的距离为x 米,试将△EMN的面积S(平方米)表示成关于x的函数;
(3)请你探究△EMN的面积S(平方米)有无最大值,若有,请求出这个最大值;若没有,请说明理由.
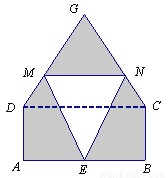
查看答案和解析>>
科目:初中数学 来源:浙江省湖州市吴兴区2017-2018学年九年级上学期期末考试数学试卷 题型:填空题
已知线段c是线段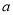 、
、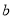 的比例中项,且
的比例中项,且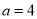 ,
, 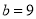 ,则线段c的长度为______.
,则线段c的长度为______.
查看答案和解析>>
科目:初中数学 来源:浙江省湖州市吴兴区2017-2018学年九年级上学期期末考试数学试卷 题型:单选题
如图,AB是⊙O的直径,C是⊙O上的一点,OD⊥BC于点D,AC=8,则OD的长为( )

A. 3 B. 4 C. 4.5 D. 5
B 【解析】∴CD=BD, ∵OA=OB,AC=8, ∴OD=AC=4. 故选:B.查看答案和解析>>
科目:初中数学 来源:2018春季学北师大版九年级数学下册期末测评试卷 题型:填空题
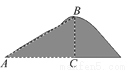
如图,某登山运动员从营地A沿坡角为30°的斜坡AB到达山顶B,如果AB=2000米,则他实际上升了________米.
查看答案和解析>>
科目:初中数学 来源:吉林省2018届九年级(上)期中数学试卷 题型:解答题
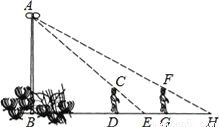
如图,花丛中有一路灯杆AB,在灯光下,大华在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时大华的影长GH=5米.如果大华的身高为2米,求路灯杆AB的高度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com