
��ͼ�٣�ֱ��y=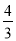 x+4����x���ڵ�A����y���ڵ�C����A��C�����������F1��x������һ��B��1��0����
x+4����x���ڵ�A����y���ڵ�C����A��C�����������F1��x������һ��B��1��0����
��1����������F1����ʾ�Ķ��κ����ı���ʽ��
��2������M��������F1λ�ڵڶ�����ͼ����һ�㣬���AMC��������ʱ��M�����꼰S��AMC�����ֵ��
��3����ͼ�ڣ���������F1��y�ᷭ�۲������ơ��õ�������F2����A��B�루2��������ĵ�M�Ķ�Ӧ��ֱ�ΪA�䡢B�䡢M�䣬����M����M��E��x���ڵ�E����ֱ��A��C�ڵ�D����x�����Ƿ���ڵ�P��ʹ����A�䡢D��PΪ��������������AB��C���ƣ������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
��1��y=��x2��x+4�� ��2����a=��ʱ��S��AMC�����ֵ�����ֵΪ9����ʱ��M������5���� ��3������A�䡢D��PΪ��������������AB��C����ʱ����P������Ϊ��2��0������0���� �������������������1������һ�κ����Ľ���ʽ�����A��C�����꣬Ȼ��������B�����꼴��������κ����Ľ���ʽ����2������M��������F1�ϣ����Կ���M��a����a2��a+4����Ȼ��ֱ����S�ı�... ǧ�������������ĩ�����Ծ�����ϵ�д�
ǧ�������������ĩ�����Ծ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2018�˽̰���꼶��ѧ�²���ϰ�����д����� ���ͣ������
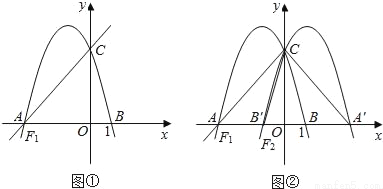
��ͼ1���ڡ�ABC�У���֪��BAC��45�㣬AD��BC��D��BD��2��DC��3����AD�ij�. СƼͬѧ���������Գ�֪ʶ����ͼ�ν��з��۱任��ͼ1.���ֱ���AB��ACΪ�Գ��ᣬ������ABD����ACD����Գ�ͼ�Σ�D��ĶԳƵ�ΪE��F���ӳ�EB��FC�ཻ��G�㣬�õ��ı���AEGF��������.��AD=x�����ù��ɶ�������������x�ķ���ģ�ͣ��������x��ֵ.�ο�СƼ��˼·��̽������������⣺��ͼ2���ڡ�ABC�У���BAC��30�㣬AD��BC��D��AD��4.���㰴��СƼ�ķ�����ͼ,�õ��ı���AEGF�����BGC���ܳ�.����ͼ������ĸ��ͼ1�е���ĸ��Ӧ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ�����꼶�ϲ���ѧȫ���ۺϲ��Ծ� ���ͣ���ѡ��
����������y=kx��yֵ��x���������С����˺�����ͼ����������
A. һ�������� B. һ�������� C. ���������� D. ����������
D ��������������������y=kx��yֵ��x���������С�� �ຯ����ͼ������������.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ�����ѧ���꼶�²��һ��1.3ͬ�����ݵij�����ʱ��ϰ ���ͣ������
(2a)3��(2a)m���ڣ� ��
A. 3(2a)m-4 B. (2a)m-1 C. (2a)3-m D. (2a)m+1
C ����������������� ��ѡC.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ�����ѧ���꼶�²��һ��1.3ͬ�����ݵij�����ʱ��ϰ ���ͣ���ѡ��
���������ȷ���ǣ� ��
A. b6 ��b5= 2b5 B. b5 + b5 = b10 C. x15��x5 = x25 D. y10��y5 = y5
D �����������������A��������b�� B��������2b5��C��������x10 ;��D����ȷ. ��ѡD.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ��ɳ��2017-2018ѧ����꼶���ϣ���һ���¿���ѧ�Ծ� ���ͣ������
Ϊ����������������������ϰ�ʱ��õĽ�ͨ���ߵ�����������ȡ�����в���������е��飬Ҫ�����ߴӡ�A�����г���B���綯����C����������D����ͥ������E�����������ѡ����ѡ����õ�һ������е�������������Ƴ����²�����������ͳ��ͼ������ͳ��ͼ������ͳ��ͼ�ش��������⣺
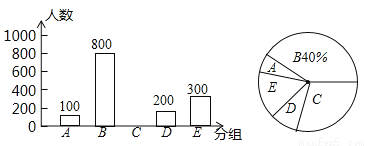
��1������ε����У�һ�������� ����������ͳ��ͼ�У�C���Ӧ������Բ�Ľ��� �㣻
��2���벹ȫ����ͳ��ͼ��
��3�����ס��������ϰ�ʱ��A��B��C��D���ֽ�ͨ���������ѡ��һ�֣���ס�������ǡ��ѡ��ͬһ�ֽ�ͨ�����ϰ�ĸ����Ƕ��٣����û���״ͼ���б�����⣮
��1��2000��108����2����ͼ����������3���� �������� �����������1������B��������Լ��ٷֱȣ����ɵõ�������������������ó�C����������ٸ�������Բ�ĽǵĶ���=����ռ����İٷֱȡ�360����м��㼴�ɣ� ��2������C�����������ȫ����ͳ��ͼ�� ��3�����ݼס��������ϰ�ʱ��A��B��C��D���ֽ�ͨ���������ѡ��һ�ֻ���״ͼ���б����������ø��ʹ�ʽ�õ��ס�������ǡ��ѡ��...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ��ɳ��2017-2018ѧ����꼶���ϣ���һ���¿���ѧ�Ծ� ���ͣ������
��ʽ�֡�������
2x2��18=_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ�����ѧ���꼶�²� ��1�� ��ʽ�ij˳� �½ڼ���� ���ͣ������
������ʽ�ij˷���ʽ���㣮
(1)299��301��1;
(2)1122��113��111.
��1��90000��2��1 ��������������(1)����ƽ���ʽ���㼴�ɣ���2��ԭʽ���κ�����ƽ���ʽ����ȥ���źϲ����ɵó����. ��������� (1)ԭʽ��(300��1)(300��1)��1��3002��1��1��90000 (2)ԭʽ��1122��(112��1)(112��1)��1122��1122��1��1�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ������꼶��ѧ�²� �ڶ��� �ཻ����ƽ���� 2.1 ����ֱ�ߵ�λ�ù�ϵ ͬ����ϰ�� ���� ���ͣ���ѡ��
��֪�Ϧ�����ǣ��Ϧ���Ϧ»������Ϧ���Ϧû��࣬��Ϧ£��Ϧõ�ֵ����( )
A. 45�� B. 60�� C. 90�� D. 180��
C ��������������������ݻ�������֮��Ϊ90�㣬��������֮��Ϊ180�㣬������⼴�ɵó��𰸣� �������� ������ã��Ϧ�+�Ϧ�=180�㣬�Ϧ�+�Ϧ�=90�㣬 ��ʽ����ɵã��Ϧ©��Ϧ�=90�㣮 ��ѡ��C���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com