
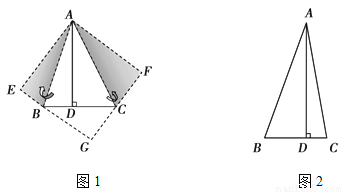
如图1,在△ABC中,已知∠BAC=45°,AD⊥BC于D,BD=2,DC=3,求AD的长. 小萍同学灵活运用轴对称知识,将图形进行翻折变换如图1.她分别以AB、AC为对称轴,画出△ABD、△ACD的轴对称图形,D点的对称点为E、F,延长EB、FC相交于G点,得到四边形AEGF是正方形.设AD=x,利用勾股定理,建立关于x的方程模型,即可求出x的值.参考小萍的思路,探究并解答新问题:如图2,在△ABC中,∠BAC=30°,AD⊥BC于D,AD=4.请你按照小萍的方法画图,得到四边形AEGF,求△BGC的周长.(画图所用字母与图1中的字母对应)
科目:初中数学 来源:2017-2018 北师大版数学八年级下册 第二章 一元一次不等式和一元一次不等式组 单元检测卷 题型:单选题
(2017江苏省宿迁市,第5题,3分)已知4<m<5,则关于x的不等式组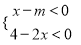 的整数解共有( )
的整数解共有( )
A. 1个 B. 2个 C. 3个 D. 4个
B 【解析】解不等式x-m<0,可得x<m,解4-2x<0,可得x>2,又由于不等式组有解,可得其解集为2<x<m,由于4<m<5,所以其整数解为3、4,所以共有2个. 故选:B.查看答案和解析>>
科目:初中数学 来源:人教版初中数学七年级下册第八章《实际问题与二元一次方程组》同步练习 题型:单选题
若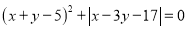 ,则x、y的值分别为( )
,则x、y的值分别为( )
A. 7,7 B. 8,-3 C. 8,3 D. 以上结论都不对
B 【解析】根据非负项和为0,则每一项都为0,可得 解得 所以x、y的值分别为8,-3. 故选B.查看答案和解析>>
科目:初中数学 来源:人教版初中数学七年级下册第八章《消元解二元一次方程组》同步练习 题型:单选题
方程组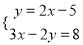 消去y后所得的方程是( )
消去y后所得的方程是( )
A. 3x-4x+10=8 B. 3x-4x+5=8 C. 3x-4x-5=8 D. 3x-4x-10=8
A 【解析】试题分析: , ①代入②得:3x-2(2x-5)=8, 3x-4x+10=8. 故选A.查看答案和解析>>
科目:初中数学 来源:人教版初中数学七年级下册第八章《消元解二元一次方程组》同步练习 题型:单选题
已知关于x、y的方程组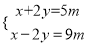 的解满足3x+2y=19,则m的值为( )
的解满足3x+2y=19,则m的值为( )
A. 1 B. 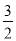 C. 5 D. 7
C. 5 D. 7
查看答案和解析>>
科目:初中数学 来源:2018人教版八年级数学下册练习:期中达标检测卷 题型:填空题
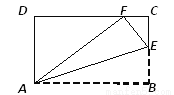
如图所示,将矩形ABCD沿AE向上折叠,使点B落在DC边上的F处,若△AFD的周长为9,△ECF的周长为3,则矩形ABCD的周长为___________.
查看答案和解析>>
科目:初中数学 来源:2018人教版八年级数学下册练习:期中达标检测卷 题型:单选题
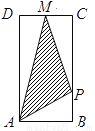
在矩形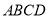 中,
中, 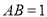 ,
, 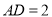 ,
, 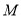 是
是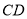 的中点,点
的中点,点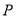 在矩形的边上沿
在矩形的边上沿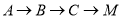 运动,则
运动,则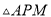 的面积
的面积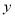 与点
与点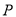 经过的路程
经过的路程 之间的函数关系用图象表示大致是下图中的( )
之间的函数关系用图象表示大致是下图中的( )
A. 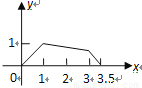 B.
B. 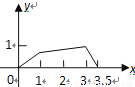 C.
C. 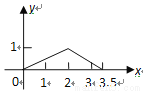 D.
D. 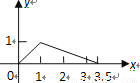
查看答案和解析>>
科目:初中数学 来源:北师大版八年级上册数学全册综合测试卷 题型:填空题
已知点P(3,2)在一次函数 的图象上,则b=____________.
的图象上,则b=____________.
查看答案和解析>>
科目:初中数学 来源:湖南省长沙市2017-2018学年九年级(上)第一次月考数学试卷 题型:解答题
如图①,直线y=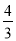 x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
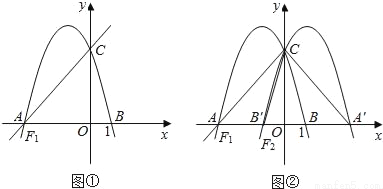
(1)求抛物线F1所表示的二次函数的表达式.
(2)若点M是抛物线F1位于第二象限图象上一点,求△AMC的面积最大时点M的坐标及S△AMC的最大值.
(3)如图②,将抛物线F1沿y轴翻折并“复制”得到抛物线F2,点A、B与(2)中所求的点M的对应点分别为A′、B′、M′,过点M′作M′E⊥x轴于点E,交直线A′C于点D,在x轴上是否存在点P,使得以A′、D、P为顶点的三角形与△AB′C相似?若存在,请求出点P的坐标;若不存在,请说明理由.
(1)y=﹣x2﹣x+4; (2)当a=﹣时,S△AMC有最大值,最大值为9,此时,M(﹣,5); (3)当以A′、D、P为顶点的三角形与△AB′C相似时,点P的坐标为(2,0)或(﹣,0). 【解析】试题分析:(1)利用一次函数的解析式求出点A、C的坐标,然后再利用B点坐标即可求出二次函数的解析式;(2)由于M在抛物线F1上,所以可设M(a,﹣a2﹣a+4),然后分别计算S四边...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com