
若关于x的分式方程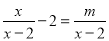 有增根,则m的值为__________.
有增根,则m的值为__________.
科目:初中数学 来源:黄金30题系列 八年级数学 小题好拿分 题型:填空题
点A(﹣4,3)关于x轴的对称点的坐标是______.
(﹣4,﹣3). 【解析】试题分析:根据关于x轴对称的点,横坐标相同,纵坐标互为相反数进行解答.点A(﹣4,3)关于x轴的对称点的坐标是(﹣4,﹣3),故答案为:(﹣4,﹣3).查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题七年级北师大版数学试卷(A卷) 题型:解答题
某同学在A、B两家超市发现他看中的随身听的单价相同,书包单价也相同.随身听和书包单价之和是452元,且随身听的单价是书包单价的4倍少8元.
(1)求该同学看中的随身听和书包的单价各是多少元?
(2)某假期该同学上街,恰好赶上商家促销,超市A所有商品打八折销售,超市B全场购满100元返购物券30元(销售不足100元不返券,购物券全场通用),但他只带了400元钱,如果他只在一家超市购买看中的这两样物品,你能说出他可以选择在哪一家购买吗?若两家都可以选择,在哪一家购买更省钱?
(1)92,360;(2) 在超市A购买更省钱. 【解析】试题分析:(1)根据随身听和书包单价之和是452元,列方程求解即可; (2)根据两商家的优惠方式分别计算是否两家都可以选择,比较钱数少的则购买更省钱. 试题解析:(1)设书包单价为x元,则随身听的单价为(4x-8)元. 根据题意,得4x-8+x=452, 解得:x=92,4x-8=4×92-8=360. ...查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题七年级北师大版数学试卷(A卷) 题型:单选题
n等于1,2,3,…时,由白色小正方形和黑色小正方形组成的图形分别如图所示,则第n个图形中白色小正方形和黑色小正方形的个数总和是(用n表示,n是正整数)( )
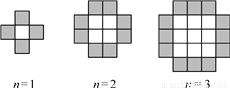
A. n+4 B. 4n+8 C. n2+4n D. n2+n
C 【解析】第1个图形:白色正方形1个,黑色正方形4×1=4个,共有1+4=5个; 第2个图形:白色正方形22=4个,黑色正方形4×2=8个,共有4+8=12个; 第3个图形:白色正方形32=9个,黑色正方形4×3=12个,共有9+12=21个; …, 第n个图形:白色正方形n2个,黑色正方形4n个,共有n2+4n个。 故答案为:C.查看答案和解析>>
科目:初中数学 来源:黄金30题系列 八年级数学 小题好拿分 题型:填空题
如图,已知在△ABC中,AB=AC,AD=8cm,BC=12cm,点E、F都在中线AD上,连接EB、EC、FB、FC,则图中阴影部分的面积为______.
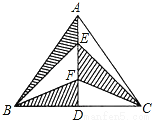
查看答案和解析>>
科目:初中数学 来源:黄金30题系列 八年级数学 小题好拿分 题型:填空题
若(x+k)(x-4)的展开式中不含有x的一次项,则k的值为_________.
4 【解析】试题分析:原式=+(k-4)x-4k,根据题意得:k-4=0,解得:k=4.查看答案和解析>>
科目:初中数学 来源:黄金30题系列 八年级数学 小题好拿分 题型:单选题
如图,请仔细观察用直尺和圆规作一个角∠A′O′B′等于己知角∠AOB的示意图,根据所学知识,说明∠A′O′B′=∠AOB的依据是( )
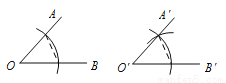
A. SSS B. SAS C. ASA D. AAS
A 【解析】试题分析:根据作图过程可知O′C′=OC,O′D′=OD,C′D′=CD,所以运用的是三边对应相等,两三角形全等作为依据. 故选:A.查看答案和解析>>
科目:初中数学 来源:黄金30题系列 八年级数学 大题易丢分 题型:解答题
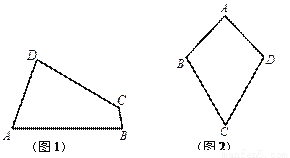
定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.
(1)已知:如图1,四边形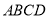 是“等对角四边形”,
是“等对角四边形”, 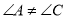 ,
, 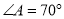 ,
, 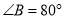 .求
.求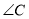 ,
, 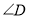 的度数.
的度数.
(2)在探究“等对角四边形”性质时:
① 小红画了一个“等对角四边形”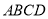 (如图2),其中
(如图2),其中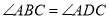 ,
, 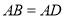 ,此时她发现
,此时她发现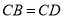 成立.请你证明此结论.
成立.请你证明此结论.
② 由此小红猜想:“对于任意‘等对角四边形’,当一组邻边相等时,另一组邻边也相等”.你认为她的猜想正确吗?若正确,请证明;若不正确,请举出反例.
(3)已知:在“等对角四边形”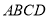 中,
中, 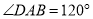 ,
, 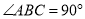 ,AB=AD=4,.求∠D和对角线
,AB=AD=4,.求∠D和对角线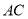 的长.
的长.
查看答案和解析>>
科目:初中数学 来源:浙江杭州拱墅区文澜中学2018届九年级上学期期中考试数学试卷(含解析) 题型:解答题
如图,在平面直角坐标系中,抛物线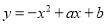 交
交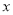 轴于点
轴于点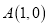 ,
, 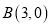 两点,点
两点,点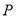 是抛物线上在第一象限内的一点,直线
是抛物线上在第一象限内的一点,直线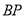 与
与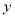 轴相交于点
轴相交于点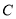 .
.
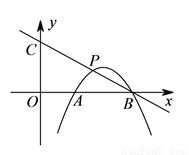
(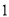 )当点
)当点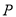 是线段
是线段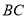 的中点时,求点
的中点时,求点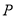 的坐标.
的坐标.
(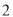 )在(
)在(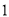 )的条件,求
)的条件,求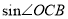 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com