
A��B�����������ϵ�λ����ͼ��ʾ�����е�A��Ӧ��������Ϊ-4����AB=10������P�ӵ�A��������ÿ��2����λ���ȵ��ٶ��������������˶������˶�ʱ��Ϊt�루t��0����

��1����t=1ʱ��AP�ij�Ϊ_________����P��ʾ��������Ϊ______��
��2����PB=2ʱ����t��ֵ��
��3��MΪ�߶�AP���е㣬NΪ�߶�PB���е㣮 �ڵ�P�˶��Ĺ����У��߶�MN�ij����Ƿ����仯�����仯����˵�����ɣ������䣬���㻭��ͼ�Σ�������߶�MN�ij���
��1��2��-2����2��4��6����3�����Ȳ����ҳ�Ϊ5�� �������������������1�����ݵ�P���˶��ٶȣ������������2����PB=2ʱ��Ҫ������������ۣ���P�ڵ�B���������Ҳࣻ��3�������е�Ķ����������߶εij��Ȳ���. �����������1����Ϊ��P���˶��ٶ�ÿ��2����λ���ȣ����Ե�t=1ʱ��AP�ij�Ϊ2����Ϊ��A��Ӧ��������Ϊ-4��AP=2�����Ե�P��ʾ��������Ϊ-2����2����PB=2ʱ��...
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017�갲��ʡ�Ϸ��и�������ѧУ�п���ѧģ���Ծ� ���ͣ������
��ͼ��AB��AC��BD�ǡ�O�����ߣ�P��C��DΪ�е㣬���AB=5��AC=3����BD�ij�Ϊ_____��
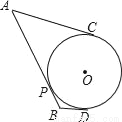
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ���һѧ����ĩ��ϰ����֮����ϰģ�������꼶��ʦ�����ѧ�Ծ���C���� ���ͣ������
��ͼ����A��ԭ����������������˶���ͬʱ����BҲ��ԭ����������������˶���3s���������18����λ���ȣ���֪��B���ٶ��ǵ�A���ٶȵ�5��(�ٶȵ�λ����λ���ȣ�s)��
��1�������A����B�˶����ٶȣ����������ϱ��A��B�����ԭ������˶�3sʱ��λ�ã�
��2����A��B�����(1)�е�λ�ÿ�ʼ������ԭ�����ٶ�ͬʱ�����������˶�������ʱ��ԭ��ǡ�ô��ڵ�A����B�����м�?
��3����A��B�����(2)�е�λ�ü�����ԭ�����ٶ������������˶���ͬʱ����һ��C��ԭ��λ��Ҳ���A�˶�����������A�������������B�˶���������B���������������A�˶������������ֱ����B�ϵ�Aʱ����C����ֹͣ�˶�������Cһֱ��8����λ���ȣ�s���ٶ������˶������C�ӿ�ʼ�˶���ֹͣ�˶�����ʻ��·���Ƕ��ٸ���λ����?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ���һѧ����ĩ��ϰ����֮����ϰģ�������꼶��ʦ�����ѧ�Ծ���C���� ���ͣ���ѡ��
��֪����A��B��C��ͬһ��ֱ���ϣ���M��N�ֱ���AB��AC���е㣬���AB=10cm��AC=8cm����ô�߶�MN�ij���Ϊ��������
A. 6cm B. 9cm C. 3cm��6cm D. 1cm��9cm
D �����������������������������ٵ�C��AB�ϣ��ڵ�C��AB���ӳ����ϣ���������������߶ε��е�����ʣ��ɵ�BM��BN�ij����������߶εĺ͡���ɵó��𰸣� �������� ��1����C���߶�AB�ϣ��磺 ��M���߶�AB���е㣬��N���߶�BC���е㣬 MB=AB=5��BN=CB=4�� MN=BM-BN=5-4=1cm�� ��2����C��...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ���һѧ����ĩ��ϰ����֮����ϰģ�������꼶��ʦ�����ѧ�Ծ���C���� ���ͣ���ѡ��
��ͼ��ʾͼ���У������������չ��ͼ���ǣ�������
A. 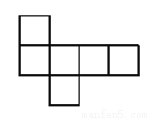 B.
B. 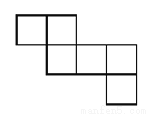
C. 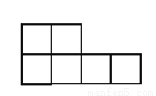 D.
D. 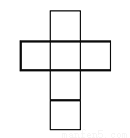
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ���һѧ����ĩ��ϰ����֮����ϰģ�������꼶��ʦ�����ѧ�Ծ���A���� ���ͣ������
������x�ķ��̣�k��2��x|k��1|+5k+1=0 ��һԪһ�η��̣���k+x=_____��
����������������ã�k-2��0��|k-1|=1�� ��ã�k=0�� ��k=0���뷽�̵�-2x+1=0�� ��ã�x= ��k+x=. �ʴ���: .�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ���һѧ����ĩ��ϰ����֮����ϰģ�������꼶��ʦ�����ѧ�Ծ���A���� ���ͣ���ѡ��
��ͼ��ֱ��AB��CD�ཻ�ڵ�O������OMƽ�֡�AOC����MON��90�㣬����AOM��35�㣬���CON�Ķ���Ϊ( )
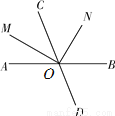
A. 35�� B. 45�� C. 55�� D. 65��
C ��������������OMƽ�֡�AOC����AOM=35�㣬 ���MOC=35��. �ߡ�MON=90��. ���CON=��MON-��MOC=90��-35��=55��. ��ѡC.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���ƽ�30��ϵ�� ���꼶��ѧ С����÷� ���ͣ������
����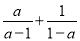 =______��
=______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�Ϸ���2016-17ѧ��ȵ�һѧ����ĩ��ѧ����������꼶��ѧ�Ծ� ���ͣ������
��ͼ��ʱ�������dz������������Ʒ�������̺���������ѧ֪ʶ.

��1������֪���������ʱ��ת��һ�ܶ��� �ȣ�����ת��һ���� ���ӣ�ʱ��ת��һ����12Сʱ������720���ӣ����ԣ�����ÿ����ת�� �ȣ�ʱ��ÿ����ת�� ��.
��2����5:00��5:30��������ʱ���ת���˶��ٶȣ�
��3�������÷���֪ʶ���ͣ���1:00��ʼ����1:00��2:00֮�䣬�Ƿ����ij��ʱ�̣�ʱ���������ͬһ��ֱ���ϣ��������ڣ�˵�����ɣ������ڣ������1:00��ʼ�����ʱ�䣬ʱ���������ͬһ��ֱ����.
��1��360��60��6��0.5.��2��15�㣻��3���������ӻ����ʱ���������ͬһ��ֱ����. �������������������1�������ӱ��̵��������.����һ�����ֳ�60��С��ÿһ��С�����ԽǵĶ�����6�㣻 ��2����5:00��5:30������ת����30����ʱ��ת����2.5��������⣻ ��3��ʱ���������ͬһ��ֱ���ϣ�������������ٷ�����ʱ���غϣ��ڷ�����ʱ���180�㣬 ���δ֪...�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com