
如图,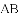
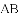
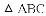
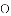
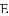
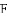
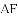
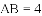
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源:黄金30题系列 九年级数学 大题好拿分 题型:解答题
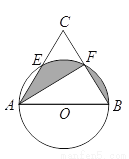
△ABC的内切圆⊙o与BC,CA,AB分别相切于点D、E、F,且AB=9cm,BC=14cm,CA=13cm,求AF、BD、CE的长?
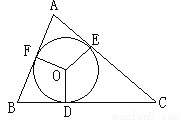
查看答案和解析>>
科目:初中数学 来源:2017年广西防城港市中考数学模拟试卷 题型:填空题
如图所示,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第n个图形需要黑色棋子的个数是___________.
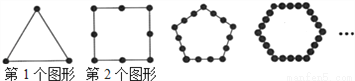
查看答案和解析>>
科目:初中数学 来源:2017年广西防城港市中考数学模拟试卷 题型:单选题
下列说法正确的是( )
A. 有理数的绝对值一定是正数
B. 如果两个数的绝对值相等,那么这两个数相等
C. 如果一个数是负数,那么这个数的绝对值是它的相反数
D. 绝对值越大,这个数就越大
C 【解析】试题分析:根据有理数的绝对值为:正数的绝对值为本身,0的绝对值为0,负数的绝对值为其相反数,故A不正确; 根据正数的绝对值为正数,负数的绝对值为其相反数,故B不正确; 根据负数的绝对值为其相反数,故C正确; 当这个数为负数时,绝对值越大,这个数越小,故D不正确. 故选:C查看答案和解析>>
科目:初中数学 来源:黄金30题系列 九年级数学 小题好拿分 题型:填空题
如图,大楼AD高30m,远处有一塔BC,某人在楼底A处测得塔顶的仰角为60°,爬到楼顶D测得塔顶的仰角为30°,则塔高BC为_________m.
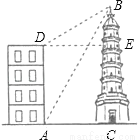
查看答案和解析>>
科目:初中数学 来源:黄金30题系列 九年级数学 小题好拿分 题型:单选题
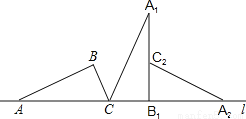
如图,把直角△ABC的斜边AC放在定直线l上,按顺时针的方向在直线l上转动两次,使它转到△A2B2C2的位置,设AB=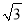 ,BC=1,则顶点A运动到点A2的位置时,点A所经过的路线为( )
,BC=1,则顶点A运动到点A2的位置时,点A所经过的路线为( )
A. (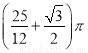 B.
B. 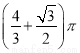 C. 2π D.
C. 2π D. 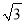 π
π
查看答案和解析>>
科目:初中数学 来源:黄金30题系列 九年级数学 小题好拿分 题型:单选题
如图:∠C=90°,∠DBC=30°,AB=BD,利用此图可求得tan75°的值是( )
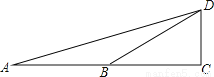
A. 2﹣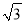 B. 2+
B. 2+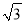 C.
C. 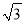 ﹣2 D.
﹣2 D. 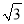 +1
+1
查看答案和解析>>
科目:初中数学 来源:安徽省芜湖市教育集团2017-2018学年度上学期八年级第二次月考 题型:填空题
已知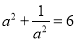 ,则
,则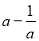 的值是______.
的值是______.
查看答案和解析>>
科目:初中数学 来源:2018年春人教版八年级数学下册(广西)期中测试 题型:解答题
如图1,在正方形ABCD中,点E,F分别在AB,BC上,且AE=BF.
(1)试探索线段AF,DE的数量关系,写出你的结论并说明理由;
(2)连接EF,DF,分别取AE,EF,FD,DA的中点H,I,J,K,则四边形HIJK是什么特殊四边形?请在图2中补全图形,并说明理由.
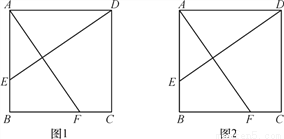
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com