
不等式组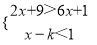 的解集为x<2,则k的取值范围为( )
的解集为x<2,则k的取值范围为( )
A. k>1 B. k<1 C. k≥1 D. k≤1
C 【解析】【解析】 解不等式组,得: .∵不等式组的解集为x<2,∴k+1≥2,解得k≥1.故选C.科目:初中数学 来源:四川省自贡市2017-2018学年上学期期末考试八年级数学试卷 题型:单选题
若二次三项式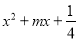 为完全平方式,则m的值为( )
为完全平方式,则m的值为( )
A. ±2 B. 2 C. ±1 D. 1
C 【解析】试题解析: 是完全平方式. 解得: 故选C.查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学下册(人教版):期末检测题(二) 题型:填空题
如图所示,在?ABCD中,E,F为对角线BD上的两点,要使四边形AECF为平行四边形,在不连接其他线段的前提下,还需要添加的一个条件是_____.
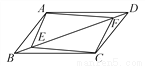
查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学下册(华师大版):期末检测2 题型:解答题
解不等式组 ,把不等式组的解集在数轴上表示出来,并写出不等式组的非负整数解.
,把不等式组的解集在数轴上表示出来,并写出不等式组的非负整数解.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学下册(华师大版):期末检测2 题型:填空题
不等式组 的解集是x>-1,则a的取值范围是______.
的解集是x>-1,则a的取值范围是______.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学下册(华师大版):期末检测2 题型:单选题
下列说法中错误的是( )
A. 能够重合的图形称为全等图形 B. 全等图形的形状和大小都相同
C. 所有正方形都是全等图形 D. 形状和大小都相同的两个图形是全等图形
C 【解析】解:A.能够重合的图形称为全等图形,说法正确,故本选项错误; B.全等图形的形状和大小都相同,说法正确,故本选项错误; C.所有正方形不一定都是全等图形,说法错误,故本选项正确; D.形状和大小都相同的两个图形是全等图形,说法正确,故本选项错误; 故选C.查看答案和解析>>
科目:初中数学 来源:辽宁省抚顺县2018届九年级上学期期末教学质量检测数学试卷 题型:解答题
如图,已知等腰三角形ABC的底角为30°,以BC为直径的⊙O与底边AB交于点D,过D作DE⊥AC,垂足为E.
(1)证明:DE为⊙O的切线;
(2)连接OE,若BC=4,求△OEC的面积.
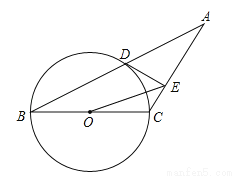
查看答案和解析>>
科目:初中数学 来源:辽宁省抚顺县2018届九年级上学期期末教学质量检测数学试卷 题型:单选题
如图,⊙O的直径AB垂直于弦CD,垂足是E,∠A=30°,CD=6,则圆的半径长为( )
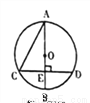
A. 2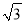 B. 2 C. 4
B. 2 C. 4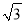 D.
D. 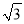
查看答案和解析>>
科目:初中数学 来源:2017-2018学年福建省龙岩市上杭县城区片三校七年级(上)联考数学试卷 题型:填空题
规定一种运算“※”,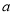 ※
※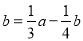 ,则方程
,则方程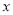 ※2=1※
※2=1※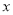 的解为________.
的解为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com