
命题“在角的内部,到角的两边距离相等的点在角的平分线上”的逆命题是:________
角平分线上的点到角的两边距离相等 【解析】命题“在角的内部,到角的两边距离相等的点在角的平分线上”的逆命题是“角平分线上的点到这个角两边的距离相等”.科目:初中数学 来源:甘肃省武威市2017-2018学年八年级(上)期中数学试卷 题型:单选题
如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变.请试着找一找这个规律,你发现的规律是( )
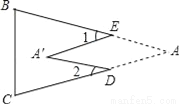
A. ∠A=∠1+∠2 B. 2∠A=∠1+∠2 C. 3∠A=2∠1+∠2 D. 3∠A=2(∠1+∠2)
B 【解析】试题分析:利用三角形的内角和及平角的定义进行求解. 【解析】 设, , 则, ∵, , ∴, , , ∴. 2∠A=∠1+∠2. 故选B.查看答案和解析>>
科目:初中数学 来源:2017年广东省韶关市南雄市中考数学模拟试卷 题型:填空题
如图:小亮从A点出发,沿直线前进10米后向左转30度,再沿直线前进10米,又向左转30度,??照这样走下去,他第一次回到出发点A点时,一共走了______米?
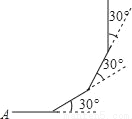
查看答案和解析>>
科目:初中数学 来源:河南省2017-2018学年八年级上期末模拟数学试卷 题型:解答题
化简:|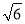 ﹣
﹣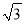 |﹣|3﹣
|﹣|3﹣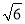 |.
|.
查看答案和解析>>
科目:初中数学 来源:河南省2017-2018学年八年级上期末模拟数学试卷 题型:填空题
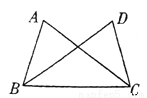
如图,AC=BD,要使△ABC≌△DCB,需添加的一个条件是 (只添一个条件即可).
查看答案和解析>>
科目:初中数学 来源:河南省2017-2018学年八年级上期末模拟数学试卷 题型:填空题
如图,已知AB∥CD,O是∠ACD和∠BAC的平分线的交点,若AC=6,S△AOC=6则AB与CD之间的距离是( ) 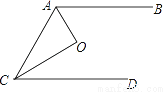
A. 1cm B. 2cm C. 3cm D. 4cm
C 【解析】过点0作AB的垂线,交AB于点D,交CD于点F,过O作OE垂直AC,交AC于点E,由题意得:OD=OE=OF, 6OE=12,解得OE=2,则DF=4.查看答案和解析>>
科目:初中数学 来源:山东省德州市2017-2018学年九年级上学期期中考试数学试卷 题型:解答题
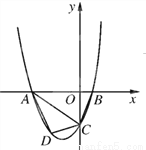
已知,如图抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A, B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,过点D做x轴的垂线,交AC于点E,求线段DE的最大值.
(3)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值.
查看答案和解析>>
科目:初中数学 来源:山东省德州市2017-2018学年九年级上学期期中考试数学试卷 题型:单选题
如图,在正方形ABCD中,E为DC边上的点,连接BE,将△BCE绕点C顺时针方向旋转90°得到△DCF,连接EF,若∠BEC=60°,则∠EFD的度数为_____度.
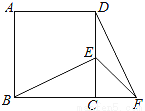
查看答案和解析>>
科目:初中数学 来源:江西省2017-2018学年度八年级第三次月考数学试卷 题型:解答题
解下列关于x的不等式(组):
(1) 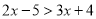 (2)
(2)
(3)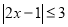 (4)
(4) 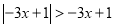
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com