
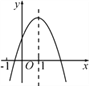
��֪���κ�����ͼ����ͼ�������н�������ȷ���У�������
��a��b��c��0����a��b��c��0����b��0����b��2a����abc��0.
A. 5�� B. 4�� C. 3�� D. 2��
���𰸡�B
�������������������x=1ʱ��y=a+b+c���������꣨1��a+b+c����
��ͼ���֪�����������ڵ�һ���ޣ�
��a+b+c��0���ʢ���ȷ��
��x=-1ʱ��y=a-b+c��
��ͼ���֪����x=-1ʱ������Ӧ�ĵ��ڵ������ޣ�
��y=a-b+c��0���ʢ���ȷ��
��ͼ�����£�
��a��0��
��x=-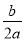 =1��
=1��
��b=-2a���ʢܴ���
��b��0���ʢ���ȷ��
��ͼ����y��Ľ�����y����ϰ��ᣬ
��c��0��
��abc��0���ʢ���ȷ��
����ȷ����4����
��ѡB��
�����͡���ѡ��
��������
10
��ͼ���ڡ�ABC�У���B����C��36�㣬AB�Ĵ�ֱƽ���߽�BC�ڵ�D����AB�ڵ�H��AC�Ĵ�ֱƽ���߽�BC�ڵ�E����AC�ڵ�G������AD��AE�������н��۴������( )
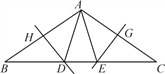
A. 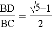 B. AD��AE����BAC���ȷ�
B. AD��AE����BAC���ȷ�
C. ��ABE�ա�ACD D. S��ADH��S��CEG

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ���㶫ʡ��ͷ��2018���п���ѧģ���Ծ������� ���ͣ���ѡ��
����������ȷ���ǣ�������
A. a2•a3=a6 B. ��2a��2=��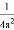 C. ����a2��3=a5 D. a2+2a2=3a2
C. ����a2��3=a5 D. a2+2a2=3a2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������2018�������ѧ�п���ϰ �ۺ���ϰ�� ���� ���ͣ������
��2��3��4���������ų�һ����λ�������ų�������ż���ĸ���Ϊ________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�������2018�������ѧ�п���ϰ�ۺϼ���� ���ͣ������
��֪����ͼ��һ�κ���y=kx+b��k��bΪ������k��0����ͼ����x�ᡢy��ֱ���A��B���㣬���뷴��������y=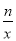 ��nΪ������n��0����ͼ���ڵڶ������ڵ�C��CD��x�ᣬ��ֱΪD����OB=2OA=3OD=6��
��nΪ������n��0����ͼ���ڵڶ������ڵ�C��CD��x�ᣬ��ֱΪD����OB=2OA=3OD=6��
��1����һ�κ����뷴���������Ľ���ʽ��
��2����������ͼ�����һ���������ꣻ
��3��ֱ��д������ʽ��kx+b�� �Ľ⼯��
�Ľ⼯��

���𰸡���1��y=��2x+6��  ����2����5����4������3����2��x��0��x��5��
����2����5����4������3����2��x��0��x��5��
�������������������1�������A��B��C���꣬�����ô���ϵ����ȷ����������ʽ��
��2�����������Ľ���ʽ��Ϊ�����飬�ⷽ���鼴�ɽ�����⣮
��3������ͼ��һ�κ�����ͼ���ڷ���������ͼ����·������ɽ�����⣬ע��Ⱥţ�
�����������1����OB=2OA=3OD=6����OB=6��OA=3��OD=2����CD��OA����DC��OB����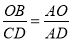 ����
���� ����CD=10�����C���꣨��2��10����B��0��6����A��3��0������
����CD=10�����C���꣨��2��10����B��0��6����A��3��0������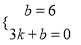 ��ã�
��ã�  ����һ�κ���Ϊy=��2x+6��
����һ�κ���Ϊy=��2x+6��
�߷���������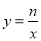 ������C����2��10������n=��20���෴������������ʽΪ
������C����2��10������n=��20���෴������������ʽΪ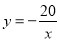 ��
��
��2���� �����
�����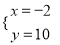 ��
��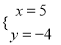 ������һ����������Ϊ��5����4����
������һ����������Ϊ��5����4����
��3����ͼ���֪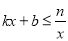 �Ľ⼯����2��x��0��x��5��
�Ľ⼯����2��x��0��x��5��

���㣺������������һ�κ����Ľ������⣮
�����͡������
��������
22
һ����װ����״��С����ͬ���ĸ�С��ÿ��С���ϸ�����һ�����֣��ֱ���1��4��7��8���ֹ涨�Ӵ�����ȡһ��С��Ӧ��������Ϊһ����λ���ĸ�λ����Ȼ��С��Żش��в�������ȣ�����ȡһ��С��Ӧ��������Ϊ�����λ����ʮλ����
��1��д���������涨�õ����п��ܵ���λ����
��2������Щ��λ������ȡһ������������ƽ��������4��С��7�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�������2018�������ѧ�п���ϰ�ۺϼ���� ���ͣ������
��ͼ����ƽ���ı���ABCD�۵���ʹ��C���A�غϣ���ʱ��D����D1���ۺ�ΪEF������BAE=55�㣬���D1AD=__��
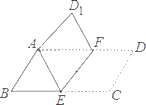
���𰸡�55�㣮
�������������������֪�ı���ABCD��ƽ���ı��Σ���ƽ���ı��ε����ʿɵá�BAD=��C�������۵������ʵá�D1AE=��C�����ԡ�D1AE=��BAD�����ɵá�D1AD=��BAE=55�㣻
���㣺ƽ���ı��ε����ʣ��۵�������.
�����͡������
��������
15
��ͼ�Ǵ����ڸ��ٹ�·ˮƽ�����ϵĽ�ͨ��ʾ�ƣ��������õ��������ݣ�AM��4�ף�AB��8�ף���MAD��45�㣬��MBC��30�㣬��ʾ�Ƶĸ�CDΪ����.�������ȷ��0.1�ף��ο����ݣ� 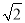 ��1.41��
��1.41�� 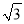 ��1.73��
��1.73��
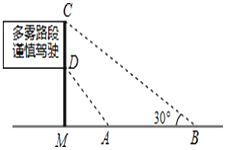
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�������2018�������ѧ�п���ϰ�ۺϼ���� ���ͣ���ѡ��
��ͼ��ֱ��l1��l2��CD��AB�ڵ�D����1=50�㣬���BCD�Ķ���Ϊ��������

A. 50�� B. 45�� C. 40�� D. 30��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���Ĵ�ʡ2018����꼶��ѧ�ڶ������ѧ�Ծ� ���ͣ������
��2017�㽭ʡ�����У���23�⣬10�֣�������������֮��֮�ƣ�ijˮ����ֳ��Ϊ�˸��õط��Ӽ������ƣ�һ�����չ���20000kg��ˮ�㣬�ƻ���ֳһ��ʱ����ٳ��ۣ���֪ÿ������ķ�����ͬ������10����ܳɱ�Ϊ30.4��Ԫ������20����ܳɱ�Ϊ30.8��Ԫ���ܳɱ�=�����ܷ���+�չ��ɱ�����
��1����ÿ��ķ���������a��Ԫ���չ��ɱ�Ϊb��Ԫ����a��b��ֵ��
��2����������ˮ�����t��������Ϊm��kg�������۵���ΪyԪ/kg���������������֪��m��t�ĺ�����ϵΪ ��y��t�ĺ�����ϵ��ͼ��ʾ��
��y��t�ĺ�����ϵ��ͼ��ʾ��
�ٷֱ������0��t��50��50��t��100ʱ��y��t�ĺ�����ϵʽ��
���轫������ˮ�����t���һ���Գ�����������ΪWԪ����tΪ��ֵʱ��W���������ֵ��������=�����ܶ�ܳɱ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���Ĵ�ʡ2018����꼶��ѧ�ڶ������ѧ�Ծ� ���ͣ���ѡ��
������ԭ�� ΪԲ�ģ����뾶Ϊ2��Բ����ֱ��
ΪԲ�ģ����뾶Ϊ2��Բ����ֱ�� ��
�� �ཻ����
�ཻ���� ��ȡֵ��Χ�ǣ� ��
��ȡֵ��Χ�ǣ� ��
A.  B.
B. 
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�ܿ���������2017-2018ѧ�����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ������
 ��ƽ������ ____________.
��ƽ������ ____________.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com