
有五张正面分别标有数字﹣2,﹣1,0,1,2的卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中随机抽取一张,记卡片上的数字为a,则使关于x的一元二次方程x2﹣2(a﹣1)x+a(a﹣3)=0有两个不相等的实数根,且以x为自变量的二次函数y=x2﹣(a2+1)x﹣a+2的图象不经过点(1,0)的概率是__________.
【解析】试题分析:∵使关于x的一元二次方程x2-2(a-1)x+a(a-3)=0有两个不相等的实数根, ∴[-2(a-1)]2-4×1×a(a-3)>0, 解得:a>-1, ∵以x为自变量的二次函数y=x2-(a2+1)x-a+2的图象不经过点(1,0), ∴12-(a2+1)-a+2≠0, ∴a≠1且a≠-2, ∴满足条件的a只有0和2, ∴使关于x的一... 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源:重庆市江津区2016-2017学年八年级下学期期末考试数学试卷 题型:单选题
分式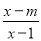 中,当
中,当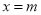 时,下列说法正确的是( )
时,下列说法正确的是( )
A. 分式的值为零 B. 分式无意义
C. 若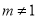 时,分式的值为零 D. 若
时,分式的值为零 D. 若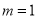 时,分式的值为零
时,分式的值为零
查看答案和解析>>
科目:初中数学 来源:2017年广东省河源市中考数学一诊试卷 题型:解答题
某商场销售的一款空调机每台的标价是1635元,在一次促销活动中,按标价的八折销售,仍可盈利9%.
(1)求这款空调每台的进价(利润率= =
=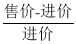 ).
).
(2)在这次促销活动中,商场销售了这款空调机100台,问盈利多少元?
(1)这款空调每台的进价为1200元;(2)商场销售这款空调机100台的盈利为10800元. 【解析】试题分析:(1)利用利润率和售价进价之间的等量关系列出方程即可; (2)用销售量乘以每台的销售利润即可. 试题解析:(1)设这款空调每台的进价为元,根据题意得: 解得: 经检验: 是原方程的解. 答:这款空调每台的进价为1200元; (2)商场销售这款空调机1...查看答案和解析>>
科目:初中数学 来源:2017年广东省河源市中考数学一诊试卷 题型:单选题
下列几何体中,俯视图为四边形的是( )
A. 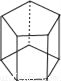 B.
B. 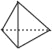 C.
C.  D.
D. 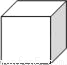
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题九年级北师大版数学试卷(C卷) 题型:解答题
已知关于 的方程
的方程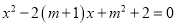 .
.
(1)若方程总有两个实数根,求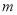 的取值范围;
的取值范围;
(2)若两实数根 、
、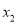 满足
满足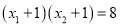 ,求
,求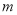 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题九年级北师大版数学试卷(C卷) 题型:单选题
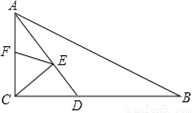
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD平分∠CAB交BC于D点,E,F分别是AD,AC上的动点,则CE+EF的最小值为( )
A. 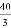 B.
B. 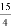 C.
C. 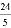 D. 6
D. 6
查看答案和解析>>
科目:初中数学 来源:北京四中2018届上学期初中九年级期中考试数学试卷 题型:解答题
在平面直角坐标系xOy中,设点P(x1,y1),Q(x2,y2)是图形W上的任意两点. 定义图形W的测度面积:若|x1-x2|的最大值为m,|y1-y2|的最大值为n,则S=mn为图形W的测度面积. 例如,若图形W是半径为l的⊙O. 当P,Q分别是⊙O与x轴的交点时,如图1,|x1-x2|取得最大值,且最大值m=2;当P,Q分别是⊙O与y轴的交点时,如图2,|y1-y2|取得最大值,且最大值n=2. 则图形W的测度而积S=mn=4.
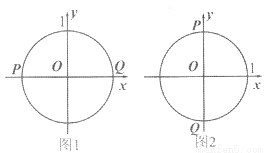
(1)若图形W是抛物线y=-x2+2x+3和直线y=2x-1围成的封闭图形,则它的测度面积S=______
(2)若图形W是一个边长为1的正方形ABCD.
①当A,B两点均在x轴上时,它的测度面积S=_________;
②此图形测度面积S的最大值为_________;
(3)若图形W是一个边长分别为3和6的矩形ABCD,求它的测度面积S的取值范围.
(1)36;(2)①1; ②2;(3)测度面积S的取值范围是18≤S≤. 【解析】试题分析:(1)先求出抛物线与直线的交点坐标,再求出抛物线的顶点坐标,然后根据定义进行计算即可得; (2)①根据给出的定义可以求出来; ②根据定义可以求出测度面积的最大值为2; (3)因为平移图形W不会改变其测度面积S的大小,将矩形ABCD的其中一个顶点B平移至x轴上,注意分三种情况讨论. ...查看答案和解析>>
科目:初中数学 来源:北京四中2018届上学期初中九年级期中考试数学试卷 题型:单选题
已知二次函数y=ax2+bx+c的图象如下图所示,则下列结论中正确的是( )
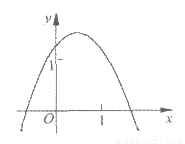
A. a>0 B. c<0 C. b2-4ac<0 D. a+b+c>0
D 【解析】由图像开口向下得a<0,当x=0时y=c>0. ax2+bx+c=0有两根所以判别式大于零.当x=1时y= a+b+c>0故选D查看答案和解析>>
科目:初中数学 来源:2017年福建省分校九年级数学综合试卷(二) 题型:解答题
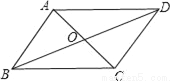
(1)如图,在□ABCD中,对角线AC、BD相交于点O.请找出图中的一对全等三角形,并给予证明;
(2)规定:一条弧所对的圆心角的度数作为这条弧的度数.
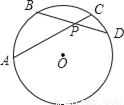
①如图,在⊙O中,弦AC、BD相交于点P,已知弧AB、弧CD分别为65°和45°,求∠APB;
②一般地,在⊙O中,弦AC、BD相交于点P,若弧AB、弧CD分别为m°和n°,求∠APB.
(用m、n的代数式表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com