
��֪���� �ķ���
�ķ���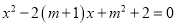 ��
��
��1����������������ʵ��������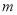 ��ȡֵ��Χ��
��ȡֵ��Χ��
��2������ʵ���� ��
��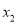 ����
����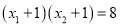 ����
����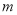 ��ֵ��
��ֵ��
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�������н�����2016-2017ѧ����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
��ͼ���ڡ�ABC�У�AB=AC��AD��BC���ϵĸߣ���E��F��AD�����ȷֵ㣬����ABC�����Ϊ12cm2����ͼ����Ӱ���ֵ������_______cm2.
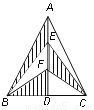
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�������н�����2017-2018ѧ����꼶��ѧ�ڵڶ�����У������ѧ�Ծ� ���ͣ���ѡ��
��������߶��У�����������ε��ǣ�������
A. 5��11��6 B. 8��8��16 C. 10��5��4 D. 6��9��14
D ��������������������������ε���������֮�ʹ��ڵ����߶Ը�ѡ������жϺ������ų�����⣮ A����5+6��11�������������Σ���Aѡ����� B����8+8=16�������������Σ���Bѡ����� C����5+4��10�������������Σ���Cѡ����� D����6+9��14��������������Σ���Dѡ����ȷ�� ��ѡ��D���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017��㶫ʡ��Դ���п���ѧһ���Ծ� ���ͣ���ѡ��
���˱��ε�ÿ���ڽ�Ϊ (����)
A. 120�� B. 135�� C. 140�� D. 144��
B ���������������������������ε��ڽ����ó�ÿ���ڽǵı�ʾ���������ɵó��𰸣� �������� �������˱��ε��ڽǹ�ʽ�ó���[��n��2����180]��n=[��8��2����180]��8=135�㣮 ��ѡ��B���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ���һѧ����ĩ��ϰ����֮����ϰģ������꼶��ʦ�����ѧ�Ծ���C���� ���ͣ������
��ͼ1����Rt��ABC�У���C=90�㣬AC=8m��BC=6m����P��C�������2m/s���ٶ����յ�A�����ƶ���ͬʱ��Q�ɵ�B������1m/s���ٶ����յ�C�����ƶ�����һ���㵽���յ�ʱ��һ����Ҳ��ֹ֮ͣ�ƶ���
��1�����������PCQ�������ACB�������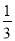 ��
��
��2���������룬��PCQ���ACB���ƣ�
��3����ͼ2����CDΪ��ACB�����ߣ���ô���˶��Ĺ����У�PQ��CD�п��ܻ��ഹֱ�����п��ܣ�����˶���ʱ�䣻��û�п��ܣ���˵�����ɣ�
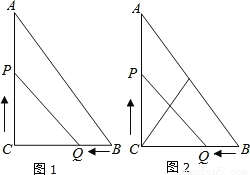
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ���һѧ����ĩ��ϰ����֮����ϰģ������꼶��ʦ�����ѧ�Ծ���C���� ���ͣ������
����������ֱ�������֩�2����1��0��1��2�Ŀ�Ƭ�����dz����ֲ�ͬ������ȫ����ͬ���ֽ����DZ��泯�ϣ�ϴ�Ⱥ���������ȡһ�ţ��ǿ�Ƭ�ϵ�����Ϊa����ʹ����x��һԪ���η���x2��2��a��1��x+a��a��3��=0����������ȵ�ʵ����������xΪ�Ա����Ķ��κ���y=x2����a2+1��x��a+2��ͼ�����㣨1��0���ĸ�����__________��
�������������������ʹ����x��һԪ���η���x2-2��a-1��x+a��a-3��=0����������ȵ�ʵ������ ��[-2��a-1��]2-4��1��a��a-3����0�� ��ã�a��-1�� ����xΪ�Ա����Ķ��κ���y=x2-��a2+1��x-a+2��ͼ�����㣨1��0���� ��12-��a2+1��-a+2��0�� ��a��1��a��-2�� ������������aֻ��0��2�� ��ʹ����x��һ...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ���һѧ����ĩ��ϰ����֮����ϰģ������꼶��ʦ�����ѧ�Ծ���C���� ���ͣ���ѡ��
��a2��4a��4�Ŀո���У��������ϡ�+�������������еõ��Ĵ���ʽ�У��ܹ�����ȫƽ��ʽ�ĸ����ǣ� ��
A. 1 B. 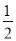 C.
C. 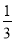 D.
D. 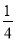
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����������2018����ѧ�ڳ��о��꼶���п�����ѧ�Ծ� ���ͣ������
��֪���κ���y=x2-2x-3.
��1������������ͼ��ĶԳ���Ͷ������꣺
��2������������ͼ����x�ᡢy��Ľ�������.
��1���Գ�����x=1�����������ǣ�1��-4���� ��2��ͼ����x�ύ�������ǣ�-l��0������3��0������y��Ľ��������ǣ�0��-3�� �������������������1�������䷽������������ʽ���ɵã� ��2���ֱ���x=0��y=0���ⷽ�̼��ɵ�. �����������1����y=x2-2x-3=��x-1��2-4�� ��Գ�����x=1�����������ǣ�1��-4���� ��2����y=0����x2-2x-...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�긣��ʡ��У���꼶��ѧ�ۺ��Ծ������� ���ͣ������
��ͼ����֪����ABCD�ı߳�AB=2��BC=3����P��AD���ϵ�һ���㣨P����A��D����Q��BC���ϵ�����һ��. ��AQ��DQ����P��PE��DQ��AQ��E����PF��AQ��DQ��F.
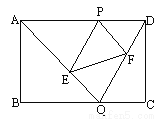
��1����֤����APE�ס�ADQ��
��2����AP�ij�Ϊx�������PEF�����S��PEF����x�ĺ�����ϵʽ������P�ںδ�ʱ��S��PEFȡ�����ֵ�����ֵΪ���٣�
��3����Q�ںδ�ʱ����ADQ���ܳ���С���������ȷ��Q�ںδ��Ĺ��̻������ظ���֤����
��1��֤��APE=��ADQ����AEP=��AQD. ע���APE�ס�ADQ���PDE�ס�ADQ����S��PEF=�� ��S��PEF==. �൱����P��AD���е�ʱ��S��PEFȡ�����ֵ. ��3����A����ֱ��BC�ĶԳƵ�A�䣬��DA�佻BC��Q���������Q����ʹ��ADQ�ܳ���С�ĵ㣬��ʱQ��BC���е�. ����������1��֤�á�APE=��ADQ����AEP=��AQD�����ɵõ���APE��...�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com