
��֪���������ε�һ�߳�Ϊ9����һ�߳�Ϊ����x2��8x��15=0�ĸ�����õ��������ε��ܳ�Ϊ________��
19��21��23 ������������������ⷽ��x2��8x+15=0��x=3��x=5�������¼���������ٵ����������ε����߳�Ϊ9��9��3ʱ�����ܳ�Ϊ21���ڵ����������ε����߳�Ϊ9��9��5ʱ�����ܳ�Ϊ23���۵����������ε����߳�Ϊ9��3��3ʱ��3+3��9�����������������߹�ϵ��������ȥ���ܵ����������ε����߳�Ϊ9��5��5ʱ�����ܳ�Ϊ19�����ϣ��õ��������ε��ܳ�Ϊ19��21��23��
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��֣�ݶ���ѧ��2017-2018ѧ����ѧ������ѧҵˮƽ���� ���꼶��ѧ�Ծ� ���ͣ������
��ʵ��a��b��c����a��b��c��0����a��b��c������y��ax��c��ͼ������� (����) ��
A. 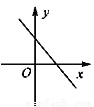 B.
B. 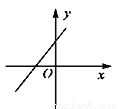 C.
C. 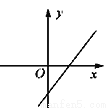 D.
D. 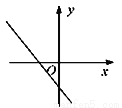
���𰸡�A
��������������ã� 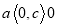 ����ѡA.
����ѡA.
�����͡���ѡ��
��������
9
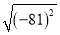 ������ƽ������____��
������ƽ������____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������� 2017-2018ѧ�� ���꼶��ѧ�ϲ� һԪ���η��� ��ʽ�ֽⷨ ר����ϰ�����𰸣� ���ͣ������
�ⷽ�̣�3x(x��2)=2(2��x).(��ʽ�ֽⷨ)
x1=����x2=2�� ��������3x(x��2) -2(2��x)=0 (3x+2)(x��2)=0�� ����3x+2=0��x��2=0�� ��� x1=����x2=2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������� 2017-2018ѧ�� ���꼶��ѧ�ϲ� һԪ���η��� ��ʽ�ֽⷨ ר����ϰ�����𰸣� ���ͣ������
��֪(a2+b2)2��(a2+b2)��6=0����a2+b2=___________��
3�� ����������(a²+b²+1)(a²+b²)?6=0�� ��(a²+b²) ²+(a²+b²)?6=0�� ��a²+b²=��,��÷��̱�Ϊ��²+��?6=0�� ��ã���=3��?2�� ��a²+b²=3��?2(��ȥ). ��a²+b²��ֵΪ3.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������� 2017-2018ѧ�� ���꼶��ѧ�ϲ� һԪ���η��� ��ʽ�ֽⷨ ר����ϰ�����𰸣� ���ͣ������
һԪ���η���x(x+3)=x�Ľ���______��
x1=0��x2=��2�� ��������������������÷ֽ���ʽ��������⣮ x��x+3��=0����x=0��x=��3�� �ʴ�Ϊ��x=0��x=��3���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������Ƭ��������ͬ��2017-2018ѧ������꼶��ѧ�ڵڶ���ѧ�������ѧ�Ծ� ���ͣ������
��ͼ��ƽ��ֱ������ϵ�У�ֱ��AB�� 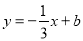 ��y���ڵ�A��0��1������x���ڵ�B������E��1��0����x��Ĵ���EF��AB�ڵ�D��P��ֱ��EF��һ���㣬���ڵ�D���Ϸ�����P��1��n����
��y���ڵ�A��0��1������x���ڵ�B������E��1��0����x��Ĵ���EF��AB�ڵ�D��P��ֱ��EF��һ���㣬���ڵ�D���Ϸ�����P��1��n����
��1��ֱ��AB�ı���ʽΪ______��
��2�����ABP��������ú�n�Ĵ���ʽ��ʾ����
��3����S��ABP=2ʱ����PBΪ���ڵ�һ����������ֱ��������BPC��ֱ��д����C�����꣮
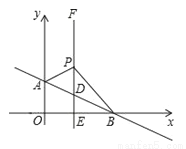
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������Ƭ��������ͬ��2017-2018ѧ������꼶��ѧ�ڵڶ���ѧ�������ѧ�Ծ� ���ͣ������
��֪y��x��2������������x=3ʱ��y=2��
��1����y��x֮��ĺ�����ϵʽ��
��2������2��x��3ʱ����y�ķ�Χ��
��1��y=2x��4����2����8��y��2�� �������������������1�������������ô���ϵ����������ã� ��2����x=-2��x=3�ֱ�������ʽ�������y �ķ�Χ. �����������1����Ϊy��x��2�����������ɵã�y=k��x��2������x=3��y=2����y=k��x��2������ã�k=2�����Խ���ʽΪ��y=2��x��2��=2x��4�� ��2����x=��2��x=3�ֱ����y=2x��4���ɵã�y=...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������Ƭ��������ͬ��2017-2018ѧ������꼶��ѧ�ڵڶ���ѧ�������ѧ�Ծ� ���ͣ���ѡ��
���㣨3��m���ں���y=
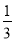 x+2��ͼ���ϣ���m��ֵΪ��������
x+2��ͼ���ϣ���m��ֵΪ��������
A. 0 B. 1 C. 2 D. 3
D ����������(3��m)�ں���y= x+2��m=,m=1,����ѡB.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ����ѧ�������г�����ѧ��ĩ�ۺϼ�� ���ͣ������
��֪����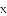
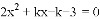 .
.
(1)��֤:��������������ȵ�ʵ����;
(2)�������һ��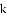
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com