练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    P为⊙O内一点，且OP=2，若⊙O的半径为3，则过点P的最短的弦是（　　）

    A. 1 B. 2 C. 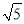D. 2

    D 【解析】试题解析： 过作弦，则是过点的最短弦，连接， 由勾股定理得： ∵， 过圆心， 故选D．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

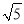
    科目：初中数学 来源：广东省江门市江海区五校2018届九年级上学期期末联考数学试卷 题型：单选题

    下列事件中是必然事件的是（ ）

    A. 打开电视，它正在播广告 B. 掷两枚质地均匀的骰子，点数之和一定大于6

    C. 某射击运动员射击一次，命中靶心 D. 早晨的太阳从东方升起

    D 【解析】A. 打开电视，它正在播广告是随机事件; B. 掷两枚质地均匀的骰子，点数之和一定大于6是不可能事件; C. 某射击运动员射击一次，命中靶心是随机事件; D. 早晨的太阳从东方升起是必然事件; 故选D.

    查看答案和解析>>

    科目：初中数学 来源：北京市顺义区2018届初三上学期期末考试数学试卷 题型：填空题

    如图标记了 △ABC与△DEF边、角的一些数据，如果再添加一个条件使△ABC∽△DEF，那么这个条件可以是__________．（只填一个即可）

    ∠C=60°（答案不唯一） 【解析】添加：∠C=60°， ∵∠A=80°=∠D，∠C=∠F=60°， ∴△ABC∽△DEF， 故答案为：∠C=60°（答案不唯一）.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年陕西安市九年级（上）期末数学试卷 题型：解答题

    某太阳能热水器的横截面示意图如图所示，已知真空热水管AB与支架CD所在直线相交于点O，且OB=OD，支架CD与水平线AE垂直，∠BAC=∠CDE=30°，DE=80cm，AC=165cm．

    （1）求支架CD的长；

    （2）求真空热水管AB的长．（结果保留根号）

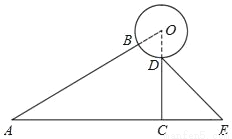
    （1）40（2）95 【解析】试题分析：（1）在中，根据 求出支架的长是多少即可． （2）首先在中，根据 求出的长是多少，进而求出的长是多少；然后求出的长是多少，即可求出真空热水管的长是多少． 试题解析：（1）在中， （2）在中，

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年陕西安市九年级（上）期末数学试卷 题型：填空题

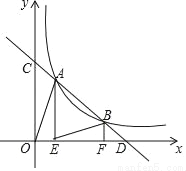
    如图，点A、B在反比例函数y=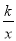（k＞0，x＞0）的图象上（点A在点B的左侧），直线AB分别交x轴，y轴于点D，C，AE⊥x轴于点E，BF⊥x轴于点F，连结AO，BE，已知AB=2BD，△AOC与△BDF的面积之和是△ABE的面积的k倍，则k的值是_____．

    【解析】试题解析：设则 即 ∴设则 故答案为： ．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年陕西安市九年级（上）期末数学试卷 题型：单选题

    如图，已知直线AB、CD被直线AC所截，AB∥CD，E是平面内任意一点（点E不在直线AB、CD、AC上），设∠BAE=α，∠DCE=β．下列各式：①α+β，②α﹣β，③180°﹣α﹣β，，④360°﹣α﹣β，∠AEC的度数可能是（　　）

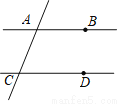
    A. ①②③ B. ①②④ C. ①③④ D. ①②③④

    B 【解析】试题解析：点有4种可能位置． （1）如图，由∥ 可得 （2）如图，过 作平行线，则由∥可得 （3）如图，由∥可得 （4）如图，由∥可得 的度数可能为 故选：D．

    查看答案和解析>>

    科目：初中数学 来源：北京市燕山区2018届初三第一学期期末数学试卷 题型：解答题

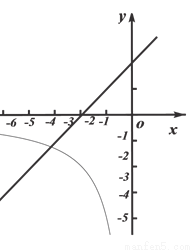
    如图，在平面直角坐标系xoy中，函数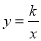（x＜0）的图象与直线y=x+2交于点A（－3，m）．

    （1）求k，m的值；

    （2）已知点P（a，b）是直线y=x上，位于第三象限的点，过点P作平行于x轴的直线，交直线y=x+2于点M，过点P作平行于y轴的直线，交函数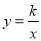（x＜0）的图象于点N．

    ①当a=－1时，判断线段PM与PN的数量关系，并说明理由；

    ②若PN≥PM结合函数的图象，直接写出b的取值范围．

    （1）k=3，m=－1；（2）①PM=PN；②-1≤b﹤0或b≤-3． 【解析】试题分析：（1）将A点代入y=x+2中即可求出m的值，然后将A的坐标代入反比例函数中即可求出k的值． （2）①当a=-1时，分别求出M、N两点的坐标即可求出PM与PN的关系； ②由题意可知：P的坐标为（b，b）(b<0)，由于PN≥PM，从而可知PN≥2，根据图象可求出b的范围． 【解析】 （...

    查看答案和解析>>

    科目：初中数学 来源：北京市2017-2018学年第一学期八年级数学期中试卷 题型：填空题

    若分式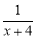在实数范围内有意义，则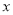的取值范围是 ．

    x≠－4. 【解析】 试题分析：对于分式而言，要使分式有意义，则必须保证分式的分母不为零，即x+4≠0，解得：x≠－4.

    查看答案和解析>>

    科目：初中数学 来源：福建省2016-2017学年八年级下学期期末考试数学试卷 题型：解答题

    如图，平行四边形ABCD，E、F两点在对角线BD上，且BE=DF，连接AE，EC，CF，FA．求证：四边形AECF是平行四边形．

    证明见解析. 【解析】 试题分析：根据两条对角线相互平分的四边形是平行四边形即可证明四边形AECF是平行四边形． 连接AC交BD于点O， ∵四边形ABCD为平行四边形， ∴OA=OC，OB=OD． ∵BE=DF，∴OE=OF． ∴四边形AECF为平行四边形．

    查看答案和解析>>

    同步练习册答案