
﹣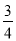 的相反数是( )
的相反数是( )
A.  B. -
B. - C. ﹣
C. ﹣ D.
D. 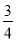
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源:辽宁省2018届九年级上学期期末考试数学试卷 题型:解答题
已知关于x的一元二次方程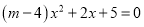 有实数根
有实数根
(1)求m的取值范围
(2)当m取最大整数值时,求出该方程的根
(1),(2) . 【解析】试题分析:(1)由关于x的一元二次方程有实数根,则m﹣4≠0且△≥0,解不等式得到m的取值范围; (2)由m的取值范围,可确定m的最大整数值,将m的最大整数值代入原方程,即可求出该方程两根. 试题解析:【解析】 (1) 由题意得:m﹣4≠0且△≥0,∵,解得 ,∴m的取值范围是且; (2)由(1)得m=3,此时方程为,即. 配方得,∴ ,...查看答案和解析>>
科目:初中数学 来源:浙江省宁波市东海实验学校2017年中考数学模拟试卷 题型:单选题
下列调查中,适合用普查方法的是( )
A、电视机厂要了解一批显象管的使用寿命
B、要了解我市居民的环保意识
C、要了解我市“阳山水蜜桃”的甜度和含水量
D、要了解你校数学教师的年龄状况
D 【解析】【解析】 A、C中的调查具有破坏性,故只能采用抽样调查,B中的调查范围大、人数多也不宜普查,而一个学校中数学老师人数不会太多,适宜普查,故选D。查看答案和解析>>
科目:初中数学 来源:2017年江苏省徐州市中考数学一模试卷 题型:填空题
函数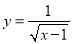 中,自变量x的取值范围是_____.
中,自变量x的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源:2017年江苏省徐州市中考数学一模试卷 题型:单选题
如图,是由几个完全相同的小正方体搭建的几何体,它的左视图是( )
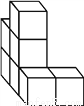
A. 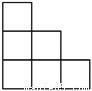 B.
B. 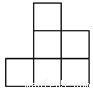 C.
C. 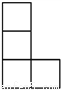 D.
D. 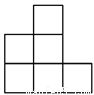
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省中考数学二模试卷 题型:解答题
某飞机模型的机翼形状如图所示,其中AB∥DC,∠BAE=90°,根据图中的数据求CD的长?(精确到1cm)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
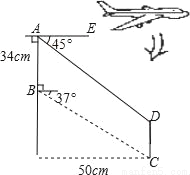
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省中考数学二模试卷 题型:填空题
若关于x的方程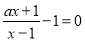 有增根,则a的值为__.
有增根,则a的值为__.
查看答案和解析>>
科目:初中数学 来源:四川省遂宁市2017-2018学年八年级上学期教学水平监测数学试卷 题型:解答题
如图,长方体底面是长为2cm 宽为1cm的长方形,其高为8cm.
(1)如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,请利用侧面展开图计算所用细线最短需要多少?
(2)如果从点A开始经过4个侧面缠绕2圈到达点B,那么所用细线最短需要多少?
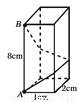
查看答案和解析>>
科目:初中数学 来源:2016-2017学年内蒙古呼伦贝尔市七年级(下)期中数学试卷 题型:填空题
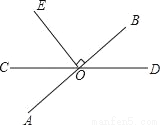
如图,直线AB、CD相交于点O,OE⊥AB于点O,且∠COE=40°,则∠BOD为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com