
如图,小华剪了两条宽为1的纸条,交叉叠放在一起,且它们较小的交角为60°,则它们重叠部分的面积为( )
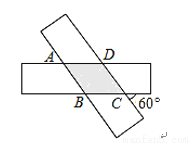
A. 3 B. 2 C. 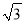 D.
D. 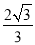
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源:重庆市江津区2016-2017学年八年级下学期期末考试数学试卷 题型:单选题
下列手机屏幕解锁图案中,不是轴对称图形的是( )
A.  B.
B.  C.
C. 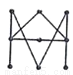 D.
D. 
查看答案和解析>>
科目:初中数学 来源:2017年广东省河源市中考数学一诊试卷 题型:单选题
如图,在正方形ABCD中,点P从点A出发,沿着正方形的边顺时针方向运动一周,则△APC的面积y与点P运动的路程x之间形成的函数关系图象大致是( )
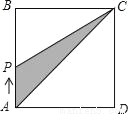
A. 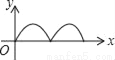 B.
B. 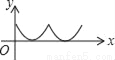 C.
C. 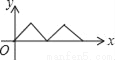 D.
D. 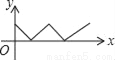
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题九年级北师大版数学试卷(C卷) 题型:填空题
如图,在△ABC中,∠C=90°,BC=16cm,AC=12cm,点P从点B出发,沿BC以2 cm /s的速度向点C移动,点Q从点C出发,以1cm/s的速度向点A移动,若点P、Q分别从点B、C同时出发,设运动时间为ts,当t=________时,△CPQ与△CBA相似.
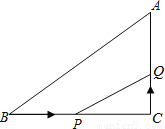
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题九年级北师大版数学试卷(C卷) 题型:单选题
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD平分∠CAB交BC于D点,E,F分别是AD,AC上的动点,则CE+EF的最小值为( )
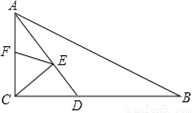
A. 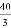 B.
B. 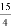 C.
C. 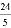 D. 6
D. 6
查看答案和解析>>
科目:初中数学 来源:北京四中2018届上学期初中九年级期中考试数学试卷 题型:解答题
问题探究:
新定义:
将一个平面图形分为面积相等的两部分的直线叫做该平面图形的“等积线”,其“等积线”被该平面图形截得的线段叫做该平面图形的“等积线段”(例如圆的直径就是圆的“等积线段”)
解决问题:
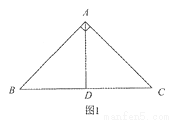
已知在Rt△ABC中,∠BAC=90°,AB=AC=2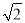 .
.
(1)如图1,若AD⊥BC,垂足为D,则AD是△ABC的一条等积线段,直接写出AD的长;
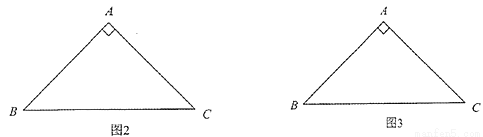
(2)在图2和图3中,分别画出一条等积线段,并直接写出它们的长度. (要求:图1、图2和图3中的等积线段的长度各不相等)
查看答案和解析>>
科目:初中数学 来源:北京四中2018届上学期初中九年级期中考试数学试卷 题型:解答题
若二次函数y=x2+bx+c的图象经过点(0,1)和(1,-2)两点,求此二次函数的表达式.
二次函数的表达式为y=x2-4x+1. 【解析】试题分析:把点(0,1)和(1,-2)分别代入二次函数的解析式,利用待定系数法进行求解即可得. 试题解析:∵二次函数y=x2+bx+c的图象经过(0,1)和(1,-2)两点, ∴ 解得 ∴二次函数的表达式为y=x2-4x+1.查看答案和解析>>
科目:初中数学 来源:2017年甘肃省张掖市中考数学三模试卷 题型:解答题
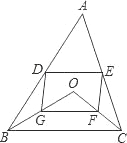
D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点.O是△ABC所在平面上的动点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.
(1)如图,当点O在△ABC的内部时,求证:四边形DGFE是平行四边形;
(2)若四边形DGFE是菱形,则OA与BC应满足怎样的数量关系?(直接写出答案,不需要说明理由.)
查看答案和解析>>
科目:初中数学 来源:2017年福建省分校九年级数学综合试卷(二) 题型:单选题
在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm.给出下列三个结论:
① 以点C为圆心,2.3cm长为半径的圆与AB相离;
② 以点C为圆心,2.4cm长为半径的圆与AB相切;
③ 以点C为圆心,2.5cm长为半径的圆与AB相交;则上述结论中正确的个数是( )
A.0个 B.1个 C.2个 D.3个
D 【解析】此题是判断直线和圆的位置关系,需要求得直角三角形斜边上的高.先过C作CD⊥AB于D,根据勾股定理得AB=5,再根据直角三角形的面积公式,求得CD=2.4.①,即d>r,直线和圆相离,正确;②,即d=r,直线和圆相切,正确;③,d<r,直线和圆相交,正确.共有3个正确. 【解析】 ①,d>r,直线和圆相离,正确; ②,d=r,直线和圆相切,正确; ③,d<r,直线和圆相...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com