
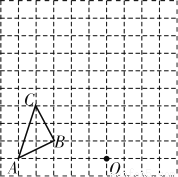
如图,在边长为1个单位长度的小正方形组成的网格中,按要求画出△A1B1C1和△A2B2C2:
(1)将△ABC先向右平移4个单位,再向上平移1个单位,得到△A1B1C1;
(2)以图中的O为位似中心,将△A1B1C1作位似变换且放大到原来的两倍,得到△A2B2C2.(在网格纸中作图)
科目:初中数学 来源:重庆市江津区2016-2017学年八年级下学期期末考试数学试卷 题型:填空题
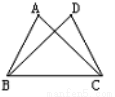
如图,∠ABC=∠DCB,请补充一个条件: ,使△ABC≌△DCB.
查看答案和解析>>
科目:初中数学 来源:2017年广东省河源市中考数学一诊试卷 题型:解答题
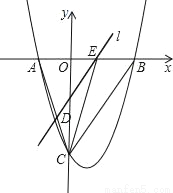
如图,抛物线y=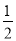 x2﹣
x2﹣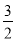 x﹣9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.
x﹣9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.
(1)求AB和OC的长;
(2)点E从点A出发,沿x轴向点B运动(点E与点A、B不重合),过点E作直线l平行BC,交AC于点D.设AE的长为m,△ADE的面积为s,求s关于m的函数关系式,并写出自变量m的取值范围;
(3)在(2)的条件下,连接CE,求△CDE面积的最大值;此时,求出以点E为圆心,与BC相切的圆的面积(结果保留π).
查看答案和解析>>
科目:初中数学 来源:2017年广东省河源市中考数学一诊试卷 题型:单选题
在平面直角坐标系中,点P(-2,-3)所在的象限是( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
C 【解析】试题解析:点P(-2,-3)的横坐标和纵坐标均为负数,所以点P(-2,-3) 在第三象限. 故选C.查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题九年级北师大版数学试卷(C卷) 题型:解答题
如图①,先把一矩形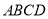 纸片上下对折,设折痕为
纸片上下对折,设折痕为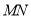 ;如图②,再把
;如图②,再把
点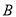 叠在折痕线
叠在折痕线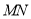 上,得到
上,得到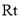
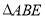 .过
.过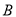 点作
点作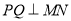 ,分别交
,分别交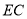 、
、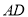 于点
于点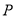 、
、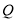 .
.
(1)求证: 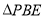 ∽
∽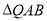 ;
;
(2)在图②中,如果沿直线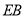 再次折叠纸片,点
再次折叠纸片,点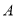 能否叠在直线
能否叠在直线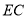 上?请说明理由;
上?请说明理由;
(3)在(2)的条件下,若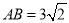 ,求
,求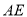 的长度.
的长度.
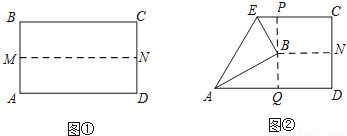
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题九年级北师大版数学试卷(C卷) 题型:填空题
已知m、n是关于x的一元二次方程x2﹣2x﹣1=0的两个实数根,则代数式3m2﹣n2﹣8m+1的值等于__________.
﹣1 【解析】试题解析:∵m、n是关于x的一元二次方程x2-2x-1=0的两个实数根, ∴m+n=-=2,mn==-1. ∴3m2-n2-8m+1=(4m2-8m)-(m2+n2)+1=-4mn-[(m+n)2-2mn]+1=4-6+1=-1.查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题九年级北师大版数学试卷(C卷) 题型:单选题
已知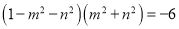 ,则m2+n2的值是( )
,则m2+n2的值是( )
A. 3 B. 3或-2 C. 2或-3 D. 2
A 【解析】, , , , ∴或(舍去), 故选A.查看答案和解析>>
科目:初中数学 来源:北京四中2018届上学期初中九年级期中考试数学试卷 题型:填空题
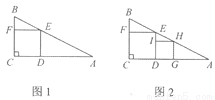
我们定义:“四个顶点都在三角形边上的正方形是三角形的内接正方形”.已知:在Rt△ABC中,∠C=90°,AC=6,BC=3.
(1)如图l,四边形CDEF是△ABC的内接正方形,则正方形CDEF的边长a1是________;
(2)如图2,四边形DGHI是(1)中△EDA的内接正方形,那么第2个正方形DGHI的边长记为a2;继续在图2中的△HGA中按上述方法作第3个内接正方形……以此类推,则第n个内接正方形的边长an=____. (n为正整数)
查看答案和解析>>
科目:初中数学 来源:2017年福建省分校九年级数学综合试卷(二) 题型:解答题
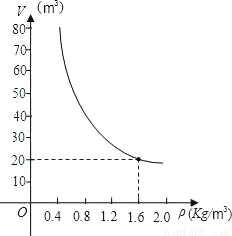
已知质量一定的某物体的体积V(m3)是密度ρ(kg/m3)的反比例函数,其图象如图所示:
(1)请写出该物体的体积V与密度ρ的函数关系式;
(2)当该物体的密度ρ=3.2Kg/m3时,它的体积v是多少?
(3)如果将该物体的体积控制在10m3~40m3之间,那么该物体的密度应在什么范围内变化?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com