练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知m、n是关于x的一元二次方程x2﹣2x﹣1=0的两个实数根，则代数式3m2﹣n2﹣8m+1的值等于__________．

    ﹣1 【解析】试题解析：∵m、n是关于x的一元二次方程x2-2x-1=0的两个实数根， ∴m+n=-=2，mn==-1． ∴3m2-n2-8m+1=（4m2-8m）-（m2+n2）+1=-4mn-[（m+n）2-2mn]+1=4-6+1=-1．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：重庆市江津区2016-2017学年八年级下学期期末考试数学试卷 题型：单选题

    一个正方形和两个等边三角形的位置如图所示，若∠3=50°，则∠1+∠2=（　　）

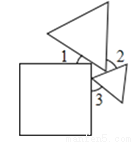
    A. 90° B. 100° C. 130° D. 180°

    B 【解析】试题解析：如图， ∠BAC=180°-90°-∠1=90°-∠1，. ∠ABC=180°-60°-∠3=120°-∠3，. ∠ACB=180°-60°-∠2=120°-∠2，. 在△ABC中，∠BAC+∠ABC+∠ACB=180°，. ∴90°-∠1+120°-∠3+120°-∠2=180°，. ∴∠1+∠2=150°-∠3，. ∵∠3=...

    查看答案和解析>>

    科目：初中数学 来源：2017年广东省河源市中考数学一诊试卷 题型：解答题

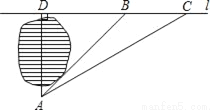
    如图，小明家在A处，门前有一口池塘，隔着池塘有一条公路l，AB是A到l的小路，现新修一条路AC到公路l，小明测量出∠ACD=30°，∠ABD=45°，BC=50m，请你帮小明计算他家到公路l的距离AD的长度（精确到0.1m；参考数据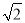： ≈1.414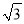， ≈1.732）

    AD≈68.3m 【解析】试题分析：根据得出进而利用解直角三角形的知识解决，注意运算的正确性． 试题解析：假设 ∵ ∴

    查看答案和解析>>

    科目：初中数学 来源：2017年广东省河源市中考数学一诊试卷 题型：单选题

    2的相反数是（　　）

    A. B. C. ﹣2 D. 2

    C 【解析】2的相反数时－2. 故选C.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年第一学期期末复习备考之精准复习模拟题九年级北师大版数学试卷（C卷） 题型：解答题

    如图，在边长为1个单位长度的小正方形组成的网格中，按要求画出△A1B1C1和△A2B2C2：

    (1)将△ABC先向右平移4个单位，再向上平移1个单位，得到△A1B1C1；

    (2)以图中的O为位似中心，将△A1B1C1作位似变换且放大到原来的两倍，得到△A2B2C2.（在网格纸中作图）

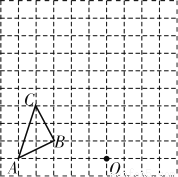
    (1)画图见解析；（2）画图见解析 【解析】试题分析：（1）根据平移的性质，找到特殊点，逐步按要求平移即可画图； （2）按照位似图形的性质，把特殊点（三角形的顶点）延位似中心扩大二倍即可. 试题解析：（1）正确图形如解图 （2）正确图形如解图

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年第一学期期末复习备考之精准复习模拟题九年级北师大版数学试卷（C卷） 题型：单选题

    如图，正方形ABCD中．点E，F分别在BC，CD上，△AEF是等边三角形．连接AC交EF于点G．过点G作GH⊥CE于点H．若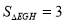，则=（　　）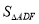

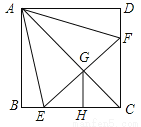
    A. 6 B. 4 C. 3 D. 2

    A 【解析】【解析】 ∵四边形ABCD是正方形，∴AB=BC=CD=AD，∠B=∠BCD=∠D=∠BAD=90°． ∵△AEF等边三角形，∴AE=EF=AF，∠EAF=60°，∴∠BAE+∠DAF=30°． 在Rt△ABE和Rt△ADF中，∵AE=AF，AB=AD，∴Rt△ABE≌Rt△ADF（HL），∴BE=DF，∵BC=CD，∴BC﹣BE=CD﹣DF，即CE=CF，∴△CE...

    查看答案和解析>>

    科目：初中数学 来源：北京四中2018届上学期初中九年级期中考试数学试卷 题型：解答题

    在平面直角坐标系xOy中，抛物线y=ax2+4ax+4a-4（a≠0）的顶点为A.

    （1）求顶点A的坐标；

    （2）过点（0，5）且平行于x轴的直线l，与抛物线y=ax2+4ax+4a-4（a≠0）交于B、C两点.

    ①当a=1时，求线段BC的长；

    ②当线段BC的长不小于8时，直接写出a的取值范围.

    （1）顶点A的坐标为（-2，-4）；（2）①线段BC的长为6；②0

    查看答案和解析>>

    科目：初中数学 来源：北京四中2018届上学期初中九年级期中考试数学试卷 题型：单选题

    已知正比例函数y=kx的图象与反比例函数y=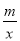的图象交于A，B两点，若点A的坐标为（-2，1），则关于x的方程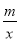=kx的两个实数根分别为（ ）.

    A. x1=-1，x2=1 B. x1=-1，x2=2 C. x1=-2，x2=1 D. x1=-2，x2=2

    D 【解析】∵正比例函数图象关于原点对称，反比例函数图象关于原点对称， ∴两函数的交点A、B关于原点对称， ∵点A的坐标为（-2，1）， ∴点B的坐标为（2，-1）， ∴关于x的方程=kx的两个实数根分别为-2、2， 故选D．

    查看答案和解析>>

    科目：初中数学 来源：2017年福建省分校九年级数学综合试卷（二） 题型：解答题

    解下列方程：

    （1）3x（x﹣1）=2﹣2x；

    （2）；

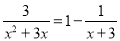    （3）先化简，后求值：（a2b）2•(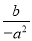)3÷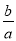（﹣）4，其中a=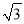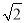（﹣）0，b=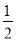（﹣）﹣2．

    （1）x1=1，x2=﹣；（2）x1=﹣1，x2=﹣3；（3）﹣4． 【解析】【试题分析】 （1）利用因式分解法解一元二次方程，3x（x﹣1）=2﹣2x， 移项得，3x（x﹣1）﹣2+2x=0；即3x（x﹣1）+2（x﹣1）=0；得（x﹣1）（3x+2）=0； 解得x1=1，x2=﹣； （2）去分母得：方程两边同乘以x（x+3）得， 3=x（x+3）﹣x，即x（...

    查看答案和解析>>

    同步练习册答案