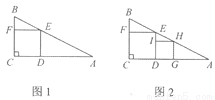
我们定义：“四个顶点都在三角形边上的正方形是三角形的内接正方形”.已知：在Rt△ABC中，∠C=90°，AC=6，BC=3.
（1）如图l，四边形CDEF是△ABC的内接正方形，则正方形CDEF的边长a1是________；
（2）如图2，四边形DGHI是（1）中△EDA的内接正方形，那么第2个正方形DGHI的边长记为a2；继续在图2中的△HGA中按上述方法作第3个内接正方形……以此类推，则第n个内接正方形的边长an=____. （n为正整数）
科目：初中数学 来源：重庆市江津区2017-2018学年八年级上学期第二次六校联考数学试卷 题型：单选题
如图所示，△ABC为等边三角形，P为BC上一点，Q为AC上一点，AQ=PQ，PR=PS，PR⊥AB于R，PS⊥AC于S，则对下面四个结论判断正确的是（ ）
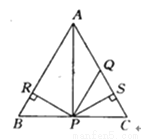
①点P在∠BAC的平分线上， ②AS=AR， ③QP∥AR， ④△BRP≌△QSP.
A. 全部正确; B. 仅①和②正确; C. 仅②③正确; D. 仅①和③正确
A 【解析】试题解析：∵PR⊥AB于R，PS⊥AC于S. ∴∠ARP=∠ASP=90°. ∵PR=PS，AP=AP. ∴Rt△ARP≌Rt△ASP. ∴AR=AS，故（2）正确，∠BAP=∠CAP. ∴AP是等边三角形的顶角的平分线，故（1）正确. ∴AP是BC边上的高和中线，即点P是BC的中点. ∵AQ=PQ. ∴点Q是AC的中点. ∴...查看答案和解析>>
科目：初中数学 来源：2017-2018学年第一学期期末复习备考之精准复习模拟题九年级北师大版数学试卷（C卷） 题型：解答题
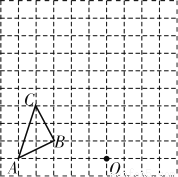
如图，在边长为1个单位长度的小正方形组成的网格中，按要求画出△A1B1C1和△A2B2C2：
(1)将△ABC先向右平移4个单位，再向上平移1个单位，得到△A1B1C1；
(2)以图中的O为位似中心，将△A1B1C1作位似变换且放大到原来的两倍，得到△A2B2C2.（在网格纸中作图）
查看答案和解析>>
科目：初中数学 来源：北京四中2018届上学期初中九年级期中考试数学试卷 题型：解答题
在平面直角坐标系xOy中，抛物线y=ax2+4ax+4a-4（a≠0）的顶点为A.
（1）求顶点A的坐标；
（2）过点（0，5）且平行于x轴的直线l，与抛物线y=ax2+4ax+4a-4（a≠0）交于B、C两点.
①当a=1时，求线段BC的长；
②当线段BC的长不小于8时，直接写出a的取值范围.
查看答案和解析>>
科目：初中数学 来源：北京四中2018届上学期初中九年级期中考试数学试卷 题型：解答题
抛物线y=ax2+bx+c上部分点的横坐标x，纵坐标y，的对应值如下表：
x | … | -2 | -1 | 0 | 1 | 2 | … |
y | … | 0 | -4 | -4 | 0 | 8 | … |
（1）根据上表填空：
①抛物线与x轴的交点坐标是_________和_________；
②抛物线经过点（-3，_________）；
（2）试确定抛物线y=ax2+bx+c的解析式.
（1）①（-2，0），（1，0）；②8；（2）所求抛物线解析式为y=2x2+2x-4. 【解析】试题分析： (1)①根据表格中函数值y=0即可得到与x轴的交点坐标； ②观察表格可知抛物线的对称轴为x=,由此可知（2，8）与（-3，8）关于对称轴对称，从而可得； （2）依题意设抛物线解析式为y=a（x+2）（x-1），代入点（0，-4）即可求得. 试题解析：（1）①观察表格可...查看答案和解析>>
科目：初中数学 来源：北京四中2018届上学期初中九年级期中考试数学试卷 题型：单选题
已知正比例函数y=kx的图象与反比例函数y=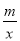
的图象交于A，B两点，若点A的坐标为（-2，1），则关于x的方程
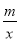=kx的两个实数根分别为（ ）.
A. x1=-1，x2=1 B. x1=-1，x2=2 C. x1=-2，x2=1 D. x1=-2，x2=2
D 【解析】∵正比例函数图象关于原点对称，反比例函数图象关于原点对称， ∴两函数的交点A、B关于原点对称， ∵点A的坐标为（-2，1）， ∴点B的坐标为（2，-1）， ∴关于x的方程=kx的两个实数根分别为-2、2， 故选D．查看答案和解析>>
科目：初中数学 来源：2017年甘肃省张掖市中考数学三模试卷 题型：解答题
如图，在平面直角坐标系中，已知矩形ABCD的三个顶点B（1，0），C（3，0），D（3，4）．以A为顶点的抛物线y=ax2+bx+c过点C．动点P从点A出发，沿线段AB向点B运动．同时动点Q从点C出发，沿线段CD向点D运动．点P，Q的运动速度均为每秒1个单位．运动时间为t秒．过点P作PE⊥AB交AC于点E．
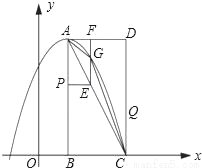
（1）直接写出点A的坐标，并求出抛物线的解析式；
（2）过点E作EF⊥AD于F，交抛物线于点G，当t为何值时，△ACG的面积最大？最大值为多少？
（3）在动点P，Q运动的过程中，当t为何值时，在矩形ABCD内（包括边界）存在点H，使以C，Q，E，H为顶点的四边形为菱形？请直接写出t的值．
（1）A（1，4）；y=﹣x2+2x+3；（2）当t=2时，S△ACG的最大值为1；（3）t=20﹣8 或t= ． 【解析】试题分析：（1）根据矩形的性质可以写出点A得到坐标；由顶点A的坐标可设该抛物线的顶点式方程为y=a（x-1）2+4，然后将点C的坐标代入，即可求得系数a的值（利用待定系数法求抛物线的解析式）；（2）利用待定系数法求得直线AC的方程y=-2x+6；由图形与坐标变换可以求得...查看答案和解析>>
科目：初中数学 来源：2017年甘肃省张掖市中考数学三模试卷 题型：填空题
分解因式：x3-4x= ______________．
x(x+2)(x-2) 【解析】分析：先提取公因式x，再对余下的多项式利用平方差公式继续分解． 详【解析】 x3﹣4x=x（x2﹣4）=x（x+2）（x﹣2）． 故答案为：x（x+2）（x﹣2）．查看答案和解析>>
科目：初中数学 来源：2017年湖北省随州市中考数学模拟试卷 题型：解答题
先化简，再求代数式（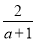
﹣
）÷
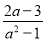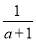的值，其中a=2sin60°+tan45°．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
