
如图,在梯形ABCD中,AB∥CD,AD=DC=CB,若∠ABD=25,则∠C=( )
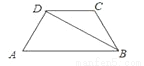
A. 130° B. 125° C. 115° D. 50°
A 【解析】∵AB∥CD, , ∴∠CDB=, ∵AD=DC=CB, ∴∠CBD=∠CDB=25°, ∴∠C=180°-25°-25°=130°. 故选A.科目:初中数学 来源:江苏省东部分校2017-2018学年七年级上学期期末考试数学试卷 题型:单选题
-2018相反数是( ).
A. 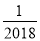 B. 2018 C.
B. 2018 C. 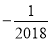 D. -2018
D. -2018
查看答案和解析>>
科目:初中数学 来源:北师大版八年级数学上册 第七章 平行线的证明 单元测试 题型:填空题
已知,如图,在△ABC中,BO和CO分别平分∠ABC和∠ACB,过O作DE∥BC,分别交AB、AC于点D、E,若BD+CE=5,则线段DE的长为________.
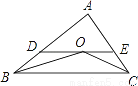
查看答案和解析>>
科目:初中数学 来源:北师大版八年级数学上册 第七章 平行线的证明 单元测试 题型:单选题
下列命题中,真命题是( )
A. 周长相等的锐角三角形都全等 B. 周长相等的直角三角形都全等
C. 周长相等的钝角三角形都全等 D. 周长相等的等腰直角三角形都全等
D 【解析】A. 周长相等的锐角三角形的对应角不一定相等,对应边也不一定相等,假命题; B. 周长相等的直角三角形对应锐角不一定相等,对应边也不一定相等,假命题; C. 周长相等的钝角三角形对应钝角不一定相等,对应边也不一定相等,假命题; D. 由于等腰直角三角形三边之比为1:1: ,故周长相等时,等腰直角三角形的对应角相等,对应边相等,故全等,真命题. 故选D.查看答案和解析>>
科目:初中数学 来源:四川省宜宾市2017-2018学年上学期期末教学质量监测八年级数学试卷 题型:解答题
任意一个正整数都可以进行这样的分【解析】
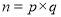 (
(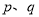 是正整数,且
是正整数,且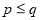 ),正整数的所有这种分解中,如果
),正整数的所有这种分解中,如果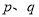 两因数之差的绝对值最小,我们就称
两因数之差的绝对值最小,我们就称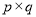 是正整数的最佳分解.并规定:
是正整数的最佳分解.并规定: 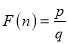 .例如24可以分解成1×24,2×12,3×8或4×6,因为
.例如24可以分解成1×24,2×12,3×8或4×6,因为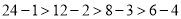 ,所以4×6是24的最佳分解,所以
,所以4×6是24的最佳分解,所以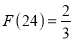 .
.
(1)求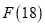 的值;
的值;
(2)如果一个两位正整数, 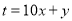 (
(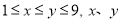 为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差记为
为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差记为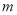 ,交换其个位上的数与十位上的数得到的新数加上原来的两位正整数所得的和记为
,交换其个位上的数与十位上的数得到的新数加上原来的两位正整数所得的和记为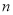 ,若
,若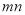 为4752,那么我们称这个数为“最美数”,求所有“最美数”;
为4752,那么我们称这个数为“最美数”,求所有“最美数”;
(3)在(2)所得“最美数”中,求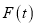 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源:四川省宜宾市2017-2018学年上学期期末教学质量监测八年级数学试卷 题型:填空题
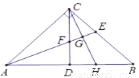
如图,在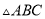 中,
中, 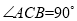 ,
, 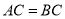 ,
, 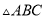 的高
的高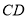 与角平分线
与角平分线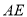 相交点
相交点 ,过点
,过点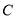 作
作 于
于 ,交
,交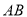 于
于 .下列说法:①
.下列说法:① ;②
;② ;③
;③ ;④
;④ ;⑤
;⑤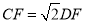 .正确的是_____.
.正确的是_____.
查看答案和解析>>
科目:初中数学 来源:北师大版数学九年级上册第二章第三节《用公式法求解一元一次方程》课时练习 题型:解答题
解方程:x2-3x-2=0
【解析】试题分析:找出a、b、c的值,代入求根公式即可. 试题解析:解:∵a=1,b=-3,c=-2;∴b2-4ac =(-3)2-4×1×(-2)=9+8=17,∴x=.查看答案和解析>>
科目:初中数学 来源:北师大版数学九年级上册第一章特殊平行四边形第二节《矩形的性质与判定》课时练习 题型:单选题
如图,矩形ABCD中,AC交BD于点O,∠AOD=60°,OE⊥AC.若AD=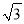 ,则OE=( )
,则OE=( )
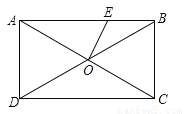
A. 1 B. 2 C. 3 D. 4
A 【解析】【解析】 ∵四边形ABCD是矩形,∠AOD=60°,∴△ADO是等边三角形,∴OA=,∠OAD=60°,∴∠OAE=30°,∵OE⊥AC,∴△OAE是一个含30°的直角三角形,∴OE=1,故选A.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com