
��֪���������ε����߳��ֱ�Ϊa+1��2a��5a��2����������������ε��ܳ���
7��5��. ��������������������������ǵ��������Σ��ɷ������������a+1=2a����a+1=5a-2����5a-2=2a����������������ֱ����a��ֵ�������ܳ�����. ��������� ��1����a+1=2aʱ����a=1,���߳��ֱ�Ϊ2,2,3���ܳ�Ϊ7 ��2����a+1=5a-2ʱ����a=,���߳��ֱ�Ϊ���ܳ�Ϊ5. ��3����5a-2=2aʱ����a=,���߳��ֱ�Ϊ,,���ܳ�Ϊ. ...
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ��ͨ��2017-2018ѧ����꼶��ѧ�ڵ������¿���ѧ�Ծ� ���ͣ������
��֪ʵ��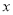 ����
����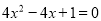 �������ʽ
�������ʽ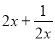 ��ֵΪ________��
��ֵΪ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�����������о��꼶���ϣ���һ���¿���ѧ�Ծ� ���ͣ������
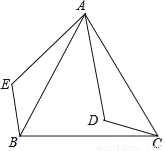
��ͼ��D�ǵȱ�������ABC��һ�㣬���߶�AD�Ƶ�A˳ʱ����ת60�㣬�õ��߶�AE������CD��BE��
��1����֤����AEB=��ADC��
��2������DE������ADC=105�㣬���BED�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�����������о��꼶���ϣ���һ���¿���ѧ�Ծ� ���ͣ���ѡ��
ƽ��ֱ������ϵ�У���P������Ϊ����5��3�������P����ԭ��ԳƵĵ�������ǣ�������
A. ��5����3�� B. ����5����3�� C. ��3����5�� D. ����3��5��
A ���������������ĶԳƵ����ʣ���֪����A(��5��3)����ԭ��ԳƵĵ������Ϊ(5����3)����ѡ��A���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�����������о��꼶���ϣ���һ���¿���ѧ�Ծ� ���ͣ���ѡ��
��ֽ���ҹ��ķ������Ļ��Ų�֮һ�����м�ֽ��Ʒ�������ĶԳ�ͼ�ε��ǣ�������
A.  B.
B.  C.
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡТ���а�У����2017-2018ѧ����꼶��ѧ�ϲ�12�������Ծ� ���ͣ������
��ͼ���ڡ�ABC�У�AB=AC��AB�Ĵ�ֱƽ����MN��AC��D�㣮��BDƽ�֡�ABC�����A=________�㣮
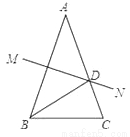
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡТ���а�У����2017-2018ѧ����꼶��ѧ�ϲ�12�������Ծ� ���ͣ���ѡ��
�����ڱ߷ֱ���ȵ��ı��ν��������Ρ�����ͼ���ı���ABCD��һ�����Σ�����AD=CD��AB=CB����̽�����ε�����ʱ���õ����½��ۣ��١�ABD�ա�CBD����AC��BD�����ı���ABCD�����=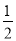 AC•BD��������ȷ�Ľ����У�������
AC•BD��������ȷ�Ľ����У�������
A. �٢� B. �٢� C. �ڢ� D. �٢ڢ�
D ���������ڡ�BDA�͡�BDC�У� �� ���BDA�ա�BDC�� �����ȷ�� ��DA=DC�� ���D��AC�Ĵ�ֱƽ�����ϣ� ��BA=BC�� ���B��AC�Ĵ�ֱƽ�����ϣ� ��BD��AC�Ĵ�ֱƽ���ߣ� �����ȷ�� �ı���ABCD�����= . �����ȷ�� ��ѡD.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㶫ʡ�����н�������У2017-2018ѧ�����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
��ͼ��ʾ��һ���й��ɵ�ͼ������1��ͼ����4������ͼ����ɣ���2��ͼ����7������ͼ��
��ɣ������� 10��ͼ���еĻ���ͼ�θ���Ϊ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017ѧ���һѧ���Ϻ��������������꼶��ѧ���������Ծ� ���ͣ������
��ͼ����Rt��ABC�У���ACB=90�㣬AC=4��BC=3��CD��б�������ߣ���E�ڱ�AC�ϣ���F�ڱ�BC�ϣ��ҡ�EDA=��FDB������EF��DC���ڵ�G��
��1������EDF=90��ʱ����AE�ij���
��2��CE = x��CF = y����y����x�ĺ�����ϵʽ����ָ��x��ȡֵ��Χ��
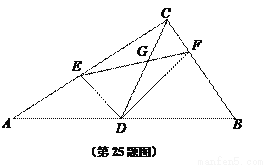
��3�������CFG�ǵ��������Σ���CF��CE�ı�ֵ��
��1������2������3��. ����������������� ����E��EH��AB�ڵ�H����DH=EH=a��tan��A=�� �ó�AH= .��Rt��ABC�У����ݹ��ɶ��������ֵ���������.����AH+HD=AD�� �������. �ֱ����E��F��AB�Ĵ��ߴ���ΪH��M������CE=x��CF=y���ó�AE=4x��CF=3y�������õ��� �� �� �� �� ������tan��EDA=tan��FDB�����ɵõ�����...�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com