
如图,在直线l上有A,B,C三点,则图中线段共有( )

A. 4条 B. 3条 C. 2条 D. 1条
B 【解析】线段有:AB、AC、BC. 故选B.科目:初中数学 来源:北师大版九年级数学(上)第二章《一元二次方程》同步测试:2.4用因式分解法求解一元二次方程 题型:填空题
方程x2=-x的解是____________.
0或-1 【解析】【解析】 ,x(x+1)=0,∴x=0或x=-1.故答案为:0或-1.查看答案和解析>>
科目:初中数学 来源:广西柳州市2017-2018学年七年级上学期期末考试数学试卷 题型:单选题
若规定:[a]表示小于a的最大整数,例如:[5]=4,[-6.7]=-7,则方程3[-π]-2x=5的解是( )
A. 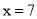 B.
B. 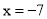 C.
C. 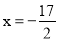 D.
D. 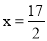
查看答案和解析>>
科目:初中数学 来源:广东省广州市天河区2017-2018学年七年级上学期期末考试数学试卷 题型:解答题
(1)计算: 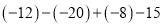 (2)计算:
(2)计算: 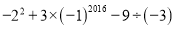
查看答案和解析>>
科目:初中数学 来源:广东省广州市天河区2017-2018学年七年级上学期期末考试数学试卷 题型:单选题
如图是含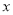 的代数式按规律排列的前4行,依此规律,若第10行第2项的值为1034,则此时
的代数式按规律排列的前4行,依此规律,若第10行第2项的值为1034,则此时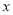 的值为( )
的值为( )
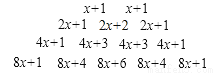
A. 1 B. 2 C. 5 D. 10
B 【解析】第1行第2项为:x+1, 第2行第2项为:2x+2, 第3行第2项为:4x+3, 第4行第2项为:8x+4, … 第n行第2项为: ·x+n. 所以第10行第2项为: ·x+10, ·x+10=1034,解得x=2. 故选B.查看答案和解析>>
科目:初中数学 来源:甘肃省天水市2018届九年级上学期期末模四考试数学试卷 题型:解答题
如图1,抛物线y=-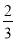 x2+bx+c与x轴相交于点A,C,与y轴相交于点B,连接AB,BC,点A的坐标为(2,0),tan∠BAO=2,以线段BC为直径作⊙M交AB于点D,过点B作直线l∥AC,与抛物线和⊙M的另一个交点分别是E,F.
x2+bx+c与x轴相交于点A,C,与y轴相交于点B,连接AB,BC,点A的坐标为(2,0),tan∠BAO=2,以线段BC为直径作⊙M交AB于点D,过点B作直线l∥AC,与抛物线和⊙M的另一个交点分别是E,F.
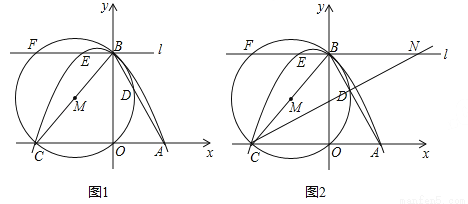
(1)求该抛物线的函数表达式;
(2)求点C的坐标和线段EF的长;
(3)如图2,连接CD并延长,交直线l于点N,点P,Q为射线NB上的两个动点(点P在点Q的右侧,且不与N重合),线段PQ与EF的长度相等,连接DP,CQ,四边形CDPQ的周长是否有最小值?若有,请求出此时点P的坐标并直接写出四边形CDPQ周长的最小值;若没有,请说明理由.
(1)抛物线的解析式为y=-x2-x+4.(2)2.(3)2+2+2. 【解析】 试题分析:(1)根据点A的坐标和tan∠BAO=2求得AO=2,BO=4,从而求得点B的坐标为(0,4),利用待定系数法求得二次函数的解析式即可. (2)首先根据抛物线的对称轴求得点A的对称点C的坐标,然后求得点B的对称点E的坐标为(-1,4),从而求得BE的长,得到EF的长即可; (3)作点...查看答案和解析>>
科目:初中数学 来源:甘肃省天水市2018届九年级上学期期末模四考试数学试卷 题型:解答题
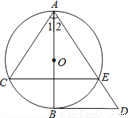
如图,AB为⊙O的直径,劣弧BC=劣弧BE,BD∥CE,连接AE并延长交BD于D.
求证:(1)AC=AE;
(2)AB2=AC•AD.
查看答案和解析>>
科目:初中数学 来源:甘肃省天水市2018届九年级上学期期末模四考试数学试卷 题型:单选题
若关于x的一元二次方程kx2﹣2x﹣1=0有两个不相等的实数根,则k的取值范围是( )
A. k>﹣1 B. k>﹣1且k≠0 C. k<1 D. k<1且k≠0
B 【解析】试题解析:∵关于x的一元二次方程kx2-2x-1=0有两个不相等的实数根, ∴k≠0且△>0,即(-2)2-4×k×(-1)>0, 解得k>-1且k≠0. ∴k的取值范围为k>-1且k≠0. 故选B.查看答案和解析>>
科目:初中数学 来源:江苏省盐城市2016-2017学年八年级上学期期末考试数学试卷 题型:填空题
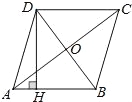
如图,菱形ABCD中,对角线AC与BD相交于点O,且AC=8,BD=6,则菱形ABCD的高DH= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com