
已知一个正数的平方根是2x和x﹣6,这个数是________ .
16. 【解析】∵一个正数的平方根是2x和x?6, ∴2x+x?6=0, 解得x=2, ∴这个数的正平方根为2x=4, ∴这个数是16. 故答案为:16.科目:初中数学 来源:湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型:填空题
点D为等边△ABC的边BC的中点,则AB:BD=________.
2:1. 【解析】【解析】 因为点D为等边△ABC的边BC的中点,所以∠BAD=30°,则AB:BD=2:1.故答案为:2:1.查看答案和解析>>
科目:初中数学 来源:2017-2018苏科版南京栖霞区七年级数学上册12月份月考试卷有答案 题型:单选题
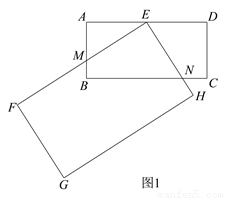
如图,C岛在A岛的北偏东50°方向,C岛在B岛的北偏西40°方向,则从C岛看A,B两岛的视角∠ACB等于 ( )

A. 90° B. 80° C. 70° D. 60°
A 【解析】如图,过点C作CG∥AE,因为AE∥BF,所以AE∥CG∥BF, 所以∠ACG=∠CAE,∠BCG=∠CBF, 因为∠CAE=50°,∠CBF=40°,∴∠ACB=∠ACG+∠BCG=50°+40°=90°. 故选A.查看答案和解析>>
科目:初中数学 来源:湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型:单选题
下列计算正确的是( )
A. 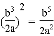 B.
B. 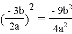
C. 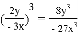 D.
D. 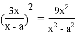
查看答案和解析>>
科目:初中数学 来源:湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型:填空题
△ABC中,DF是AB的垂直平分线,交BC于D,EG是AC的垂直平分线,交BC于E,若∠DAE=30°,则∠BAC等于________.
75°. 【解析】试题解析:如图, ∵DF是AB的垂直平分线,EG是AC的垂直平分线, ∴DA=DB,EC=EA, ∴∠B=∠BAD,∠C=∠CAE, ∵∠DAE=∠BAD+∠CAE﹣∠BAC,且∠DAE=30°, ∴30°=∠B+∠C﹣∠BAC,即30°=(180°﹣∠BAC)﹣∠BAC, 解得∠BAC=75°.查看答案和解析>>
科目:初中数学 来源:2017年山东省中考数学二模试卷 题型:解答题
问题背景
在数学活动课上,张老师要求同学们拿两张大小不同的矩形纸片进行旋转变换探究活动.如图 1,在矩形纸片ABCD 和矩形纸片EFGH中,AB=1,AD=2,且FE>AD,FG>AB,点E 是 AD 的中点,矩形纸片 EFGH 以点E 为旋转中心进行逆时针旋转,在旋转过程中会产生怎样的数量关系,提出恰当的数学问题并加以解决.
解决问题
下面是三个学习小组提出的数学问题,请你解决这些问题.
(1)“奋进”小组提出的问题是:如图 1,当 EF 与 AB 相交于点 M,EH 与 BC 相交于点 N 时,求证:EM=EN.
(2)“雄鹰”小组提出的问题是:在(1)的条件下,当 AM=CN 时,AM 与 BM 有怎样的数量关系,请说明理由.
(3)“创新”小组提出的问题是:若矩形 EFGH 继续以点 E 为旋转中心进行逆时针旋转,当 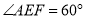 时,请你在图 2 中画出旋转后的示意图,并求出此时 EF 将边 BC 分成的两条线段的长度.
时,请你在图 2 中画出旋转后的示意图,并求出此时 EF 将边 BC 分成的两条线段的长度.

查看答案和解析>>
科目:初中数学 来源:2017年山东省中考数学二模试卷 题型:填空题
如图,将一副直角三角板如图放置,若∠AOD=18°,则∠BOC的度数为________.
查看答案和解析>>
科目:初中数学 来源:2017年江苏省苏州市中考数学三模试卷 题型:解答题
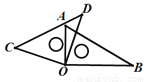
如图①,OP是∠AOB的平分线,请你利用该图形画一对以OP所在直线为对称轴的全等三角形.请你参考这个作全等三角形的方法,解答下列问题:
(1)如图②,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.请你判断并写出FE与FD之间的数量关系;
(2)如图③,在△ABC中,如果∠ACB不是直角,而(1)中的其它条件不变,请问,你在(1)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源:福建省建瓯市2018届九年级数学上册期末测试卷 题型:单选题
如图,二次函数y=ax2+bx+c(a≠0)的图象的顶点在第一象限,且过点(0,1)和(-1,0).下列结论:①ab<0;②b2>4a;③0<a+b+c<2;④0<b<1;⑤当x>-1时,y>0.其中正确结论的个数是( )
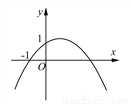
A. 5个 B. 4个 C. 3个 D. 2个
B 【解析】由抛物线的对称轴x=-在y轴右侧,可以判定a、b异号,由此确定①正确; 由抛物线与x轴有两个交点得到b2-4ac>0,又抛物线过点(0,1),得出c=1,由此判定②正确; 由a-b+c=0,及b>0得出a+b+c=2b>0;由b<1,c=1,a<0,得出a+b+c<a+1+1<2,由此判定③正确; 由抛物线过点(-1,0),得出a-b+c=0,即a=b-1,由a<0得出...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com