
已知函数y=(m﹣2)xm2+m-4 +2x﹣1是一个二次函数,求该二次函数的解析式.
【答案】y=﹣5x2+2x﹣1
【解析】试题分析:根据二次函数的定义得到m2+m﹣4=2且m﹣2≠0,由此求得m的值,进而得到该二次函数的解析式.
试题解析:依题意得:m2+m﹣4=2且m﹣2≠0. 即(m﹣2)(m+3)=0且m﹣2≠0,
解得m=﹣3,
则该二次函数的解析式为y=﹣5x2+2x﹣1
【题型】解答题
【结束】
21
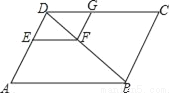
如图,在?ABCD中,EF∥AB,FG∥ED,DE:DA=2:5,EF=4,求线段CG的长.
 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(二) 题型:填空题
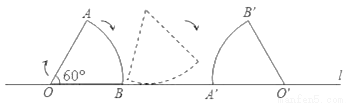
如图,将半径为2,圆心角为60°的扇形纸片AOB,在直线l上向右作无滑动的滚动至扇形A′O′B′处,则顶点O经过的路线总长为_____.
查看答案和解析>>
科目:初中数学 来源:2017年湖北省宜昌市中考数学模拟试卷(三) 题型:解答题
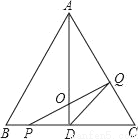
如图,在△ABC中,已知AB=BC=CA=4cm,AD⊥BC于D.点P、Q分别从B、C两点同时出发,其中点P沿BC向终点C运动,速度为1cm/s;点Q沿CA、AB向终点B运动,速度为2cm/s,设它们运动的时间为x(s).
(1)当x= 时,PQ⊥AC,x= 时,PQ⊥AB;
(2)设△PQD的面积为y(cm2),当0<x<2时,求y与x的函数关系式为 ;
(3)当0<x<2时,求证:AD平分△PQD的面积;
(4)探索以PQ为直径的圆与AC的位置关系,请写出相应位置关系的x的取值范围(不要求写出过程).
查看答案和解析>>
科目:初中数学 来源:2017年湖北省宜昌市中考数学模拟试卷(三) 题型:单选题
不等式组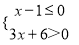 的解集为( )
的解集为( )
A. x≤1 B. x>﹣2 C. ﹣2<x≤1 D. 无解
C 【解析】试题解析: 解不等式①得,x≤1, 解不等式②得,x>-2, 所以不等式组的解集为:﹣2<x≤1. 故选C.查看答案和解析>>
科目:初中数学 来源:2017年湖北省宜昌市中考数学模拟试卷(三) 题型:单选题
﹣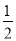 的相反数是( )
的相反数是( )
A. 2 B. 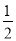 C. ﹣2 D. ﹣
C. ﹣2 D. ﹣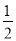
查看答案和解析>>
科目:初中数学 来源:浙江省金华市2018届九年级上册期末模拟数学试卷 题型:填空题
在一个不透明的口袋中装有8个红球和若干个白球,它们除颜色外其它完全相同,通过多次摸球试验后发现,摸到红球的频率稳定在40%附近,则口袋中白球可能有________个.
【答案】12
【解析】试题解析:设口袋中白球可能有x个,
∵摸到红球的频率稳定在40%附近,
∴口袋中摸到红色球的概率为40%,
∴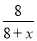 =40%,
=40%,
解得:x=12,
故答案为12.
【题型】填空题
【结束】
16
在等腰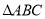 中,当顶角A的大小确定时,它的对边(即底边BC)与邻边(即腰AB或AC)的比值也确定了,我们把这个比值记作T(A),即
中,当顶角A的大小确定时,它的对边(即底边BC)与邻边(即腰AB或AC)的比值也确定了,我们把这个比值记作T(A),即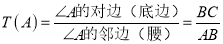 .例:T(60
.例:T(60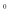 )=1,那么T(120
)=1,那么T(120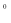 )=____________ ;
)=____________ ;
查看答案和解析>>
科目:初中数学 来源:浙江省金华市2018届九年级上册期末模拟数学试卷 题型:单选题
如图,点A,B,C在⊙O上,若∠BAC=45°,OB=2,则图中阴影部分的面积为( )
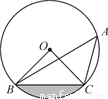
A. π-4 B.  π-1 C. π-2 D.
π-1 C. π-2 D. 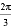 -2
-2
查看答案和解析>>
科目:初中数学 来源:2017年河北省中考数学模拟试卷 题型:填空题
如图,矩形ABCD中,AD=2,AB=5,P为CD边上的动点,当△ADP与△BCP相似时,DP=__.
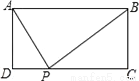
查看答案和解析>>
科目:初中数学 来源:山东省诸城市2017-2018学年七年级上期末模拟数学试卷 题型:单选题
为创建园林城市,盐城市将对城区主干道进行绿化,计划把某一段公路的一侧全部栽上桂花树,要求路的两端各栽一棵,并且每两棵树的间隔相等.如果每隔6米栽1棵,则树苗缺22棵;如果每隔7米栽1棵,则树苗正好用完.设原有树苗x棵,则根据题意列出方程正确的是( )
A. 6(x+22)=7(x-1) B. 6(x+22-1)=7(x-1)
C. 6(x+22-1)=7x D. 6(x+22)=7x
B 【解析】试题分析:设原有树苗x棵,根据首、尾两端均栽上树,每间隔6米栽一棵,则缺少22棵,可知这一段公路长为6(x+22﹣1);若每隔7米栽1棵,则树苗正好用完,可知这一段公路长又可以表示为7(x﹣1),根据公路的长度不变列出方程即可. 【解析】 设原有树苗x棵,由题意得 6(x+22﹣1)=7(x﹣1). 故选:B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com