
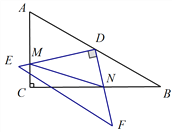
两个直角三角板如图放置,其中AC=5,BC=12,点D为斜边AB的中点.在三角板DEF绕着点D的旋转过程中,边DE与边AC始终相交于点M,边DF与边BC始终相交于点N,则线段MN的最小值为_____.
【答案】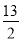
【解析】三角板DEF绕着点D的旋转过程中,四边形MCND为矩形时,根据矩形的性质可得MN=CD,此时线段MN的值最小,最小为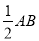 ,根据勾股定理求得AB=13,所以线段MN的最小值为
,根据勾股定理求得AB=13,所以线段MN的最小值为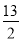 .
.
点睛:本题考查了最短路径问题,根据题意得出四边形MCND为矩形时线段MN的值最小是解题的关键.
【题型】填空题
【结束】
15
解关于x的不等式组: 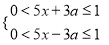 ,其中a为参数.
,其中a为参数.
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源:江苏省苏州市2017届九年级中考数学预测试卷 题型:填空题
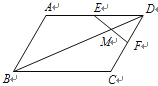
如图,在□ABCD中,E、F分别是AD、CD的中点,EF与BD相交于点M,若△DEM的面积为1,则□ABCD的面积为________.
查看答案和解析>>
科目:初中数学 来源:山东省济宁市兖州市2018届九年级中考一模试卷数学试卷 题型:解答题
(1)阅读理【解析】
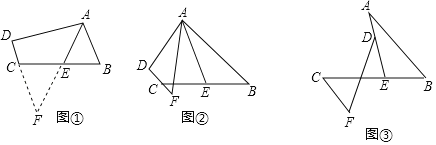
如图①,在四边形ABCD中,AB∥DC,E是BC的中点,若AE是∠BAD的平分线,试判断AB,AD,DC之间的等量关系.
解决此问题可以用如下方法:延长AE交DC的延长线于点F,易证△AEB≌△FEC,得到AB=FC,从而把AB,AD,DC转化在一个三角形中即可判断.
AB、AD、DC之间的等量关系为 ;
(2)问题探究:如图②,在四边形ABCD中,AB∥DC,AF与DC的延长线交于点F,E是BC的中点,若AE是∠BAF的平分线,试探究AB,AF,CF之间的等量关系,并证明你的结论.
(3)问题解决:如图③,AB∥CF,AE与BC交于点E,BE:EC=2:3,点D在线段AE上,且∠EDF=∠BAE,试判断AB、DF、CF之间的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源:山东省济宁市兖州市2018届九年级中考一模试卷数学试卷 题型:单选题
要使分式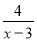 有意义,x应满足的条件是( )
有意义,x应满足的条件是( )
A. x>3 B. x=3 C. x<3 D. x≠3
查看答案和解析>>
科目:初中数学 来源:湖北省黄冈市2018届九年级中考全真模拟试卷(二)数学试卷 题型:解答题
抚顺某中学为了解八年级学生的体能状况,从八年级学生中随机抽取部分学生进行体能测试,测试结果分为A,B,C,D四个等级.请根据两幅统计图中的信息回答下列问题:
(1)本次抽样调查共抽取了多少名学生?
(2)求测试结果为C等级的学生数,并补全条形图;
(3)若该中学八年级共有700名学生,请你估计该中学八年级学生中体能测试结果为D等级的学生有多少名?
(4)若从体能为A等级的2名男生2名女生中随机的抽取2名学生,做为该校培养运动员的重点对象,请用列表法或画树状图的方法求所抽取的两人恰好都是男生的概率.
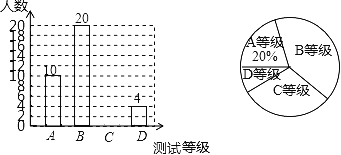
【答案】(1)50;(2)16;(3)56(4)见解析
【解析】试题分析:
(1)根据统计图中的信息可知,获得A等的有10人,占抽查总数的20%,由此即可计算出抽查学生的总数;
(2)由(1)中计算结果结合统计图中已知的A、B、D三个等级的人数即可求得C等级的人数,并由此补全条形统计图;
(3)由(1)中求得的被抽查学生的总数及获得D等级的有4人可计算出获得D等级的人数所占的百分比,即可求得800人中可能获得D等级的人数;
(4)设两名男生为A1、A2,两名女生为B1、B2,画出树形图分析即可求得所求概率;
试题解析:
(1)10÷20%=50(名)
答:本次抽样调查共抽取了50名学生.
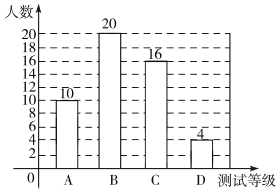
(2)50-10-20-4=16(名)
答:测试结果为C等级的学生有16名.
图形统计图补充完整如下图所示:
(3)700×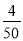 =56(名)
=56(名)
答:估计该中学八年级学生中体能测试结果为D等级的学生有56名.
(4)画树状图法:设体能为A等级的两名男生分别为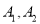 ,体能为A等级的两名女生分别为
,体能为A等级的两名女生分别为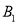 ,
,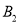 ,画树状图如下:
,画树状图如下:
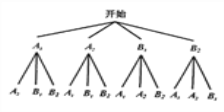
由树状图可知,共有12 种结果,每种结果出现的可能性相同,而抽取的两人都是男生的结果有两种:(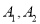 ),(
),(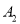 ,
,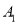 ), ∴P(抽取的两人是男生)=
), ∴P(抽取的两人是男生)=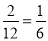 .
.
【题型】解答题
【结束】
20
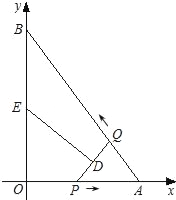
如图,在平面直角坐标系xOy中,直线AB与x轴交于点A,与y轴交于点B,且OA=3,AB=5.点P从点O出发沿OA以每秒1个单位长的速度向点A匀速运动,到达点A后立刻以原来的速度沿AO返回;点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动.伴随着P、Q的运动,DE保持垂直平分PQ,且交PQ于点D,交折线QB﹣BO﹣OP于点E.点P、Q同时出发,当点Q到达点B时停止运动,点P也随之停止.设点P、Q运动的时间是t秒(t>0).
(1)求直线AB的解析式;
(2)在点P从O向A运动的过程中,求△APQ的面积S与t之间的函数关系式(不必写出t的取值范围);
(3)在点E从B向O运动的过程中,完成下面问题:
①四边形QBED能否成为直角梯形?若能,请求出t的值;若不能,请说明理由;
②当DE经过点O时,请你直接写出t的值.
查看答案和解析>>
科目:初中数学 来源:湖北省黄冈市2018届九年级中考全真模拟试卷(二)数学试卷 题型:填空题
现在网购越来越多地成为人们的一种消费方式,刚刚过去的2015年的“双11”网上促销活动中,天猫和淘宝的支付交易额突破67000000000元,将67000000000元用科学记数法表示为_____.
查看答案和解析>>
科目:初中数学 来源:湖北省黄冈市2018届九年级中考全真模拟试卷(二)数学试卷 题型:单选题
如图,已知直线AB、CD被直线AC所截,AB∥CD,E是平面内任意一点(点E不在直线AB、CD、AC上),设∠BAE=α,∠DCE=β.下列各式:①α+β,②α﹣β,③180°﹣α﹣β,,④360°﹣α﹣β,∠AEC的度数可能是( )
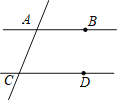
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源:湖北省潜江市2018届中考模拟题数学试卷 题型:解答题
定义:如图1,抛物线y=ax2+bx+c(a≠0)与x轴交于A,B两点,点P在该抛物线上(点P与A、B两点不重合),如果△ABP的三边满足AP2+BP2=AB2,则称点P为抛物线y=ax2+bx+c(a≠0)的勾股点.
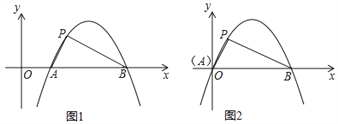
(1)直接写出抛物线y=–x2+1的勾股点的坐标;
(2)如图2,已知抛物线C:y=ax2+bx(a≠0)与x轴交于A,B两点,点P(1,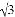 )是抛物线C的勾股点,求抛物线C的函数表达式;
)是抛物线C的勾股点,求抛物线C的函数表达式;
(3)在(2)的条件下,点Q在抛物线C上,求满足条件S△ABQ=S△ABP的Q点(异于点P)的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com