
ШчЭМЃЌгавЛПщжБНЧШ§НЧаЮжНЦЌЃЌСНжБНЧБп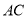 =6 cmЃЌ
=6 cmЃЌ 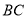 =8 cmЃЌЯжНЋжБНЧБп
=8 cmЃЌЯжНЋжБНЧБп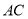 бизХжБЯп
бизХжБЯп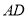 елЕўЃЌЪЙЫќТфдкаББп
елЕўЃЌЪЙЫќТфдкаББп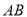 ЩЯЃЌЧвгы
ЩЯЃЌЧвгы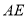 жиКЯЃЌдђ
жиКЯЃЌдђ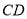 ЕФГЄЮЊ___________cmЃЎ
ЕФГЄЮЊ___________cmЃЎ

| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃКНЫеЪЁбяжнЪа2017-2018бЇФъОХФъМЖЩЯбЇЦкЦкФЉПМЪдЪ§бЇЪдОэ ЬтаЭЃКЬюПеЬт
ФГЙћдА2014ФъЫЎЙћВњСПЮЊ100ЖжЃЌ2016ФъЫЎЙћВњСПЮЊ144ЖжЃЌдђИУЙћдАЫЎЙћВњСПЕФФъЦНОљдіГЄТЪЮЊ_____ЃЎ
20% ЁОНтЮіЁПЪдЬтЗжЮіЃКИљОнЬтвтЃЌЕУ 100ЃЈ1+xЃЉ2=144ЃЌНтЗНГЬЕУx1=0.2ЃЌx2=Љ2.2ЃЎx2=Љ2.2ВЛЗћКЯЬтвтЃЌЩсШЅЃЎЙЪД№АИЮЊ20%ЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃКНЫеЪЁИНЪєГѕМЖжабЇ2017-2018бЇФъАЫФъМЖ1дТдТПМЪ§бЇЪдОэ ЬтаЭЃКНтД№Ьт
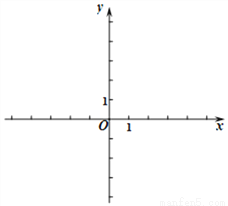
вбжЊвЛДЮКЏЪ§y1ЃНkxЃЋbЕФЭМЯёОЙ§ЕуЃЈ0ЃЌ-2ЃЉЃЌЃЈ2ЃЌ2ЃЉ.
ЃЈ1ЃЉЧѓвЛДЮКЏЪ§ЕФБэДяЪНЃЌВЂдкЫљИјжБНЧзјБъЯЕжаЛГіДЫКЏЪ§ЕФЭМЯёЃЛЃЛ
ЃЈ2ЃЉИљОнЭМЯёЛиД№ЃКЕБx ЪБЃЌy1=0ЃЛ
ЃЈ3ЃЉЧѓжБЯпy1ЃНkxЃЋbЁЂжБЯпy2ЃН-2x+4гыyжсЮЇГЩЕФШ§НЧаЮЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃКНЫеЪЁИНЪєГѕМЖжабЇ2017-2018бЇФъАЫФъМЖ1дТдТПМЪ§бЇЪдОэ ЬтаЭЃКЕЅбЁЬт
ЯТСаЬѕМўжаЃЌВЛФмХаЖЯЁїABCЮЊжБНЧШ§НЧаЮЕФЪЧЃЈ ЃЉ
A. a=1.5 b=2 c=2.5 B. aЃКbЃКc=5ЃК12ЃК13
C. ЁЯAЃЋЁЯB=ЁЯC D. ЁЯAЃКЁЯBЃКЁЯC=3ЃК4ЃК5
D ЁОНтЮіЁПA. a2+b2=1.52+22=2.52=c2ЃЌЫљвдФмХаЖЯЁїABCЪЧжБНЧШ§НЧаЮЃЌЙЪВЛЗћКЯЬтвтЃЛB. aЃКbЃКc=5ЃК12ЃК13ЃЌ52+122=132ЃЌЫљвдФмХаЖЯЁїABCЪЧжБНЧШ§НЧаЮЃЌЙЪВЛЗћКЯЬтвтЃЛC. ЁЯAЃЋЁЯB=ЁЯC ЃЌ ЁЯAЃЋЁЯB+ЁЯC =180ЁуЃЌЫљвдЁЯC=90ЁуЃЌЁїABCЪЧжБНЧШ§НЧаЮЃЌЙЪВЛЗћКЯЬтвтЃЛ D. ЁЯAЃКЁЯBЃКЁЯC=3ЃК4ЃК5ЃЌ3+4Ёй5ЃЌЫљвдЁїABCБэЪО...ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃКМЊСжЪЁЫФЦНЪа 2017-2018бЇФъЕквЛбЇЦкАЫФъМЖЪ§бЇЦкФЉзлКЯМьВтОэ ЬтаЭЃКНтД№Ьт
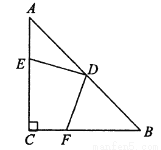
вбжЊЃКШчЭМЃЌдк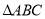 жаЃЌ
жаЃЌ 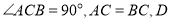 ЪЧ
ЪЧ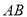 ЕФжаЕуЃЌЕу
ЕФжаЕуЃЌЕу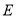 дк
дк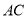 ЩЯЃЌЕу
ЩЯЃЌЕу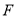 дк
дк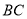 ЩЯЃЌЧв
ЩЯЃЌЧв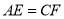 .
.
ЃЈ1ЃЉЧѓжЄЃК 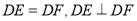 .
.
ЃЈ2ЃЉШє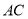 =2ЃЌЧѓЫФБпаЮ
=2ЃЌЧѓЫФБпаЮ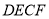 ЕФУцЛ§ЃЎ
ЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃКМЊСжЪЁЫФЦНЪа 2017-2018бЇФъЕквЛбЇЦкАЫФъМЖЪ§бЇЦкФЉзлКЯМьВтОэ ЬтаЭЃКЬюПеЬт
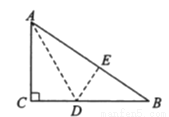
ШчЭМЃЌдкЁїABCжаЃЌAB=ACЃЌDЮЊBCжаЕуЃЌЁЯBAD=35ЁуЃЌдђЁЯCЕФЖШЪ§ЮЊ ЃЎ
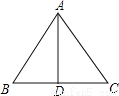
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃКМЊСжЪЁЫФЦНЪа 2017-2018бЇФъЕквЛбЇЦкАЫФъМЖЪ§бЇЦкФЉзлКЯМьВтОэ ЬтаЭЃКЕЅбЁЬт
гЩЯТСаЬѕМўВЛФмХаЖЈ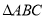 ЮЊжБНЧШ§НЧаЮЕФЪЧЃЈЁЁЁЁЃЉ
ЮЊжБНЧШ§НЧаЮЕФЪЧЃЈЁЁЁЁЃЉ
A. 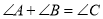 B.
B. 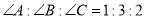
C. 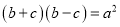 D.
D. 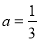 ЃЌ
ЃЌ 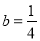 ЃЌ
ЃЌ 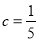
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃКЩНЖЋЪЁМУФЯЪа2018НьОХФъМЖ1дТдТПМЪ§бЇЪдОэ ЬтаЭЃКЬюПеЬт
вбжЊХзЮяЯп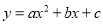 ЃЈ
ЃЈ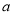 ЃМ0ЃЉЙ§AЃЈ
ЃМ0ЃЉЙ§AЃЈ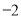 ЃЌ0ЃЉЁЂOЃЈ0ЃЌ0ЃЉЁЂBЃЈ
ЃЌ0ЃЉЁЂOЃЈ0ЃЌ0ЃЉЁЂBЃЈ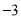 ЃЌ
ЃЌ 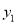 ЃЉЁЂCЃЈ3ЃЌ
ЃЉЁЂCЃЈ3ЃЌ 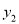 ЃЉЫФЕуЃЌдђ
ЃЉЫФЕуЃЌдђ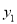 ______
______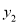 ЃЈЬюЁАЃМЁБЃЌЁА=ЁБЃЌЁАЃОЁБ ЃЉ
ЃЈЬюЁАЃМЁБЃЌЁА=ЁБЃЌЁАЃОЁБ ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃКЫФДЈЪЁУрбєЪаШ§ЬЈЯи2018НьОХФъМЖЃЈЩЯЃЉЕквЛбЇдТЪ§бЇЪдОэ ЬтаЭЃКНтД№Ьт
вбжЊЙигкxЕФвЛдЊЖўДЮЗНГЬЃКx2ЉЃЈmЉ3ЃЉxЉm=0
ЃЈ1ЃЉжЄУїдЗНГЬгаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЛ
ЃЈ2ЃЉШєХзЮяЯпy=x2ЉЃЈmЉ3ЃЉxЉmгыxжсНЛгкAЃЈx1ЃЌ0ЃЉЃЌBЃЈx2ЃЌ0ЃЉСНЕуЃЌдђAЃЌBСНЕуМфЕФОрРыЪЧЗёДцдкзюДѓЛђзюаЁжЕЃПШєДцдкЃЌЧѓГіетИіжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎЃЈгбЧщЬсЪОЃКAB=|x1Љx2|ЃЉ
ЃЈ1ЃЉжЄУїМћНтЮіЃЛЃЈ2ЃЉДцдкЃЌABгазюаЁжЕЮЊ2ЃЎ ЁОНтЮіЁПЗжЮіЃКЃЈ1ЃЉИљОнИљЕФХаБ№ЪНЃЌПЩЕУД№АИЃЛЃЈ2ЃЉИљОнИљгыЯЕЪ§ЕФЙиЯЕЃЌПЩЕУAЁЂBМфЕФОрРыЃЌИљОнЖўДЮКЏЪ§ЕФаджЪЃЌПЩЕУД№АИЃЎ БОЬтНтЮіЃК ЃЈ1ЃЉЁї=[ЉЃЈmЉ3ЃЉ]2Љ4ЃЈЉmЃЉ=m2Љ2m+9=ЃЈmЉ1ЃЉ2+8ЃЌ ЁпЃЈmЉ1ЃЉ2Ён0ЃЌ ЁрЁї=ЃЈmЉ1ЃЉ2+8ЃО0ЃЌ ЁрдЗНГЬгаСНИіВЛЕШЪЕЪ§ИљЃЛ ЃЈ2ЃЉДцдкЃЌ ...ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com