
若第二象限内的点P(x,y)满足|x|=3,y2=25,则点P的坐标是 ___________.
(-3,5) 【解析】试题分析:根据题意得出x和y的值,然后根据第二象限中点的特征得出点的坐标. 试题解析:由题意,得x=±3,y=±5. ∵点P在第二象限,∴x<0,y>0,∴x=-3,y=5,∴点P的坐标为(-3,5). 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源:浙江杭州西湖区保俶塔实验学校2018届九年级上学期期中考试数学试卷(含解析) 题型:单选题
如图, 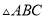 中,
中, 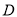 、
、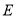 是
是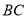 边上的点,
边上的点,  ,
,  在
在 边上,
边上,  ,
,  交
交 ,
,  于
于 ,
,  ,则
,则 等于( ).
等于( ).

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:浙江省宁波市2017-2018学年八年级上册期末模拟数学试卷 题型:填空题
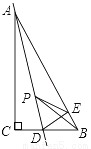
如图,在Rt△ABC中,∠C=90°,AB=5,AC=4,CB=3,点D是BC边上的点,将△ADC沿直线AD翻折,使点C落在AB边上的点E处,若点P是直线AD上的动点,则△PEB的周长的最小值是________.
查看答案和解析>>
科目:初中数学 来源:浙江省宁波市2017-2018学年八年级上册期末模拟数学试卷 题型:解答题
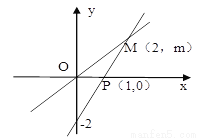
如图,一次函数y=ax+b的图像与正比例函数y=kx的图像交于点M,
(1)求正比例函数和一次函数的解析式;
(2)根据图像写出使正比例函数的值大于一次函数的值的x的取值范围;
(3)求ΔMOP的面积。
查看答案和解析>>
科目:初中数学 来源:浙江省宁波市2017-2018学年八年级上册期末模拟数学试卷 题型:填空题
等腰△ABC,其中AB=AC=17cm,BC=16cm,则三角形的面积为________cm2 .
120 【解析】利用等腰三角形的顶角的平分线、底边上的中线、底边上的高的重合的性质,勾股定理求出三角形的高AD==15cm,再利用三角形面积公式求S△ABC=BC•AD=×16×15=120cm2 . 故答案为:120.查看答案和解析>>
科目:初中数学 来源:浙江省宁波市2017-2018学年八年级上册期末模拟数学试卷 题型:单选题
如图,已知△ABC≌△EDF,点F,A,D在同一条直线上,AD是∠BAC的平分线,∠EDA=20°,∠F=60°,则∠DAC的度数是( )

A. 50° B. 60° C. 100° D. 120°
A 【解析】根据全等三角形的性质求出∠B=∠EDF=20°和∠C=∠F =60°,根据三角形内角和定理求出∠BAC=180°﹣∠B﹣∠C=100°,根据角平分线定义求出∠DAC=∠BAC=50°, 故选:A.查看答案和解析>>
科目:初中数学 来源:湖南省邵阳县黄亭市2017~2018学年九年级数学(上)期末综合检测模拟题 题型:解答题
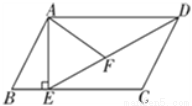
如图,在 ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6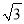 ,AF=4
,AF=4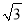 ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源:湖南省邵阳县黄亭市2017~2018学年九年级数学(上)期末综合检测模拟题 题型:单选题
如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等,若等腰直角△ABC的三个顶点分别在这三条平行直线上,则sina的值是( )
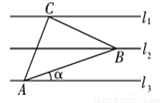
A. 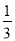 B.
B. 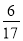 C.
C. 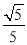 D.
D. 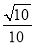
查看答案和解析>>
科目:初中数学 来源:山东省诸城市2018届九年级上学期期中联考数学试卷(Word版). 题型:解答题
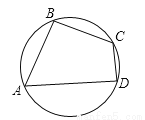
如图,在圆内接四边形ABCD中,∠A=60°,∠B=90°,AB=2,CD=1,求BC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com