
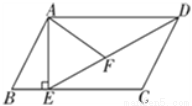
如图,在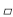 ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6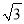 ,AF=4
,AF=4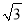 ,求AE的长.
,求AE的长.
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:初中数学 来源:山东省2017-2018学年八年级12月月考数学试卷 题型:解答题
已知一次函数的图象经过A(-2,-3),B(1,3)两点.
⑴ 求这个一次函数的解析式;
⑵ 试判断点P(-1,1)是否在这个一次函数的图象上
⑶ 求此函数与x轴、y轴围成的三角形的面积.
(1) y=2x+1;(2)不在;(3)0.25. 【解析】(1)用待定系数法求解函数解析式; (2)将点P坐标代入即可判断; (3)求出函数与x轴、y轴的交点坐标,后根据三角形的面积公式即可求解. 解答: (1)设一次函数的表达式为y=kx+b, 则-3=-2k+b、3=k+b,解得:k=2,b=1. ∴函数的解析式为:y=2x+1。 (2)将点P...查看答案和解析>>
科目:初中数学 来源:浙江省宁波市2017-2018学年八年级上册期末模拟数学试卷 题型:单选题
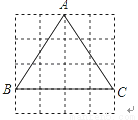
正方形网格中,△ABC如图放置,则sin∠BAC=( )
A. 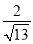 B.
B. 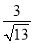 C.
C. 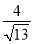 D.
D. 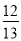
查看答案和解析>>
科目:初中数学 来源:浙江省宁波市2017-2018学年八年级上册期末模拟数学试卷 题型:填空题
若第二象限内的点P(x,y)满足|x|=3,y2=25,则点P的坐标是 ___________.
(-3,5) 【解析】试题分析:根据题意得出x和y的值,然后根据第二象限中点的特征得出点的坐标. 试题解析:由题意,得x=±3,y=±5. ∵点P在第二象限,∴x<0,y>0,∴x=-3,y=5,∴点P的坐标为(-3,5).查看答案和解析>>
科目:初中数学 来源:浙江省宁波市2017-2018学年八年级上册期末模拟数学试卷 题型:单选题
被誉为“沙漠之舟”的骆驼,其体温随着气温的变化而变化.在这个问题中,自变量是( )
A. 骆驼 B. 沙漠 C. 气温 D. 体温
C 【解析】由于体温随着气温的变化而变化,则自变量是气温,因变量是体温. 故选:C.查看答案和解析>>
科目:初中数学 来源:湖南省邵阳县黄亭市2017~2018学年九年级数学(上)期末综合检测模拟题 题型:解答题
(2016湖南省永州市)某种商品的标价为400元/件,经过两次降价后的价格为324元/件,并且两次降价的百分率相同.
(1)求该种商品每次降价的百分率;
(2)若该种商品进价为300元/件,两次降价共售出此种商品100件,为使两次降价销售的总利润不少于3210元.问第一次降价后至少要售出该种商品多少件?
(1)10%;(2)23. 【解析】试题分析:(1)设该种商品每次降价的百分率为x%,根据“两次降价后的售价=原价×(1﹣降价百分比)2”,列出方程,解方程即可得出结论;(2)设第一次降价后售出该种商品m件,则第二次降价后售出该种商品件,根据“总利润=第一次降价后的单件利润×销售数量+第二次降价后的单件利润×销售数量”表示出总利润,再根据总利润不少于3210元,即可的出关于m的一元一次不等式...查看答案和解析>>
科目:初中数学 来源:湖南省邵阳县黄亭市2017~2018学年九年级数学(上)期末综合检测模拟题 题型:填空题
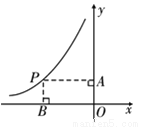
如图,点P是反比例函数y=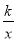 (x<0)图象上一点,PA垂直于y 轴,垂足为A,PB垂直于x轴,垂足为点B,若矩形 PBOA的面积为6,则k的值为_____.
(x<0)图象上一点,PA垂直于y 轴,垂足为A,PB垂直于x轴,垂足为点B,若矩形 PBOA的面积为6,则k的值为_____.
查看答案和解析>>
科目:初中数学 来源:2017年甘肃省兰州市中考数学模拟试卷 题型:解答题
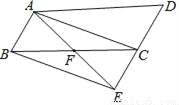
如图,延长平行四边形ABCD的边DC到点E,使CE=DC,连接AE,交BC于点F,连接AC、BE.
(1)求证:BF=CF;
(2)若AB=2,AD=4,且∠AFC=2∠D,求平行四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源:山东省诸城市2018届九年级上学期期中联考数学试卷(Word版). 题型:单选题
如图,△ABC内接于⊙O,A为劣弧BC的中点,∠BAC=120°,过点B作⊙O的直径BD,连接AD,若AD=6,则AC的长为( )
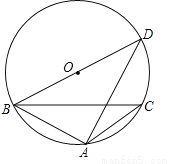
A. 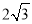 B.
B. 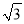 C. 2 D.
C. 2 D. 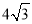
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com