
使分式 有意义,则x的取值范围是( )
有意义,则x的取值范围是( )
A. x≠1 B. x=1 C. x≤1 D. x≥1
A 【解析】试题分析:根据分式分母不为0的条件,要使在实数范围内有意义,必须.故选A. 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源:北京市2017-2018学年第一学期八年级数学期中试卷 题型:解答题
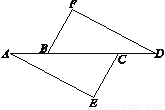
已知:如图,点A,B,C,D在一条直线上,AB=CD,AE∥FD,且∠E=∠F.求证:EC=FB.
查看答案和解析>>
科目:初中数学 来源:北京市分校2017-2018学年度第一学期期中初二数学试卷 题型:单选题
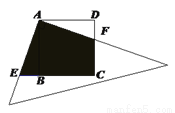
如图,正方形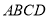 的边长为4,将一个足够大的直角三角板的直角顶点放于点A处,该三角板的两条直角边与
的边长为4,将一个足够大的直角三角板的直角顶点放于点A处,该三角板的两条直角边与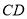 交于点F,与
交于点F,与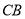 延长线交于点E.四边形
延长线交于点E.四边形 的面积是( ).
的面积是( ).
A. 16 B. 12 C. 8 D. 4
A 【解析】试题分析:根据边角边可以证明∆ABE?∆ADF,所以阴影部分的面积是正方形的面积,故阴影部分面积是16,故选A.查看答案和解析>>
科目:初中数学 来源:福建省2016-2017学年八年级下学期期末考试数学试卷 题型:填空题
若关于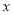 的方程
的方程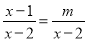 有增根,则
有增根,则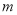 的值是___________.
的值是___________.
查看答案和解析>>
科目:初中数学 来源:福建省2016-2017学年八年级下学期期末考试数学试卷 题型:单选题
下列命题正确的是( )
A. 对角线互相平分的四边形是平行四边形
B. 对角线互相垂直的四边形是菱形
C. 对角线相等的四边形是矩形
D. 对角线互相垂直且相等的四边形是正方形
A 【解析】A. 对角线互相平分的四边形是平行四边形,说法正确; B. 对角线互相垂直的四边形是菱形,说法错误,应为对角线互相垂直且平分的四边形是菱形; C. 对角线相等的四边形是矩形,说法错误,应为对角线相等且平分的四边形是矩形; D. 对角线互相垂直且相等的四边形是正方形,说法错误,应为对角线互相垂直且相等的平行四边形是正方形; 故选:A.查看答案和解析>>
科目:初中数学 来源:上海市黄浦区2018届九年级上学期期末调研测试数学试卷(WORD版) 题型:解答题
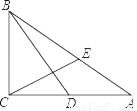
如图,在△ABC中,∠ACB=90°,AC=4,BC=3,D是边AC的中点,CE⊥BD交AB于点E.
(1)求tan∠ACE的值;
(2)求AE:EB.
查看答案和解析>>
科目:初中数学 来源:上海市黄浦区2018届九年级上学期期末调研测试数学试卷(WORD版) 题型:填空题
已知抛物线y=ax2+bx+c开口向上,一条平行于x轴的直线截此抛物线于M、N两点,那么线段MN的长度随直线向上平移而变_____.(填“大”或“小”)
大 【解析】因为二次函数的开口向上,所以点M,N向上平移时,距离对称轴的距离越大,即MN的长度随直线向上平移而变大,故答案为:大.查看答案和解析>>
科目:初中数学 来源:北京市西城外国语学校2017-2018学年度第一学期八年级数学期中试卷 题型:解答题
如图,在△ABC中,AD⊥BC于D, CE平分∠ACB分别交AB、AD于E、F两点,且BD=FD,AB=CF.求证:(1)CE AB;(2)AE=BE.
AB;(2)AE=BE.

查看答案和解析>>
科目:初中数学 来源:黑龙江省大庆市2016---2017学年度上期初三数学期末试卷 题型:填空题
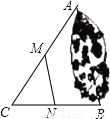
如图,A,B两点被池塘隔开,在A,B外选一点C,连接AC和BC,并分别找出AC和BC的中点M,N,如果测得MM=20m,那么A,B两点间的距离是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com