练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    几位同学用三根木棒拼成的图形如图所示,则其中符合三角形定义的是(　　)

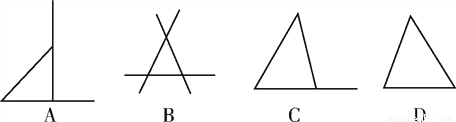
    A. A B. B C. C D. D

    D 【解析】试题分析：因为三角形是由不在同一条直线上的三条线段首尾顺次相接所成的图形． 故选D．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北师大版七年级数学下3.2 用关系式表示的变量间关系 同步练习 题型：单选题

    有一本书,每20页厚1 mm,设从第1页到第x页的厚度为y mm,则(　　)

    A. y=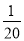x B. y=20x C. y=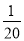+x D. y=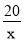

    A 【解析】∵这本书每20页厚1mm， ∴这本书每页厚为mm， ∴. 故选A.

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学七年级下册第四章4.4用尺规作三角形课时练习 题型：单选题

    如图，已知△ABC，?C＝90°，按下列要求作图（尺规作图，保留作图痕迹）：

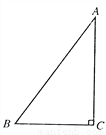
    ①作?B的平分线，与AC相交于点D；

    ②在AB边上取一点E，使BE＝BC；

    ③连结ED.

    根据所作图形，可以得到：( )

    A. AD=BD B. ?A=?CBD C. △EBD≌△CBD D. AD=BC

    C 【解析】本题作完之后的图形为： 根据作图，有?EBD=?CBD，BC=BE，又BD=BD ∴△EBD≌△CBD 故选C

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.1.1 三角形及其内角和 同步练习 题型：解答题

    如图,在△ABC中,D,E是BC,AC上的点,连接BE,AD,交于点F,问:

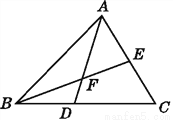
    (1)图中有多少个三角形?并把它们表示出来.

    (2)△BDF的三个顶点是什么?三条边是什么?

    (3)以AB为边的三角形有哪些?

    (4)以F为顶点的三角形有哪些?

    答案见解析 【解析】试题分析：利用三角形的定义以及三角形有关的角和边概念分别得出即可． 试题解析： （1）8个：△ABC，△ABF，△ABE，△ABD，△BDF，△AEF，△ACD，△BCE； （2）三个顶点：B，D，F；三条边：BD，BF，DF； （3）△ABC，△ABF，△ABD，△ABE； （4）△ABF，△BDF，△AEF．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.1.1 三角形及其内角和 同步练习 题型：单选题

    如图，在△ABC中，点D、E、F分别是三条边上的点，EF∥AC，DF∥AB，∠B=45°，∠C=60°．则∠EFD=（　　）

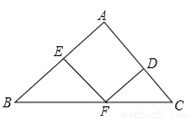
    A. 80° B. 75° C. 70° D. 65°

    B 【解析】试题分析：根据EF∥AC，求出∠EFB=∠C=60°，再根据DF∥AB，求出∠DFC=∠B=45°，从而求出∠EFD=180°﹣60°﹣45°=75°． 故选B

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.3.1 用“边边边”判定三角形全等 同步练习 题型：解答题

    如图：AB=AC，AD=AE，BE=CD，试说明：△ABD≌△ACE.

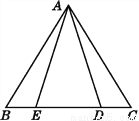
    证明见解析. 【解析】试题分析：根据等腰三角形的性质得出∠ADB=∠AEC，∠B=∠C，进而利用全等三角形的判定方法即可得出全等三角形． 试题解析： 证明：∵AD=AE， ∴∠ADE=∠AED， ∴∠ADB=∠AEC， ∵AB=AC， ∴∠B=∠C， 在△ABD和△ACE中 ∠B=∠C，∠BDA=∠CEA，AD=AE， ∴△ABD≌△AC...

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.3.1 用“边边边”判定三角形全等 同步练习 题型：单选题

    如图,在△ABC和△FED中,AC=FD,BC=ED,要利用“SSS”来判定△ABC和△FED全等时,下面的4个条件中:

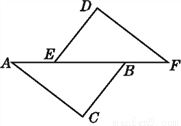
    ①AE=FB;②AB=FE;③AE=BE;④BF=BE,可利用的是(　　)

    A. ①或② B. ②或③ C. ①或③ D. ①或④

    A 【解析】由题意可得，要用SSS进行△ABC和△FED全等的判定，需要AB=FE， 若添加①AE=FB，则可得AE+BE=FB+BE，即AB=FE， 故①可以； 若添加AB=FE，则可直接证明两三角形的全等，故②可以。 若添加AE=BE，或BF=BE，均不能得出AB=FE，不可以利用SSS进行全等的证明，故③④不可以。 故选A.

    查看答案和解析>>

    科目：初中数学 来源：2017年北师大七年级下1.5《平方差公式》练习题 题型：单选题

    计算：a2-(a+1)(a-1)的结果是( )

    A. 1 B. -1 C. 2a2+1 D. 2a2-1

    A 【解析】原式=，故选A.

    查看答案和解析>>

    科目：初中数学 来源：北师大七年级下1.7 整式的除法 同步练习含答案 题型：解答题

    已知2a-b=5,求[a2+b2+2b(a-b)-(a-b)2] ÷4b的值.

    . 【解析】试题分析：原式中括号中第二项利用单项式乘以多项式法则计算，第三项利用完全平方公式展开，去括号合并得到最简结果，再利用多项式除以单项式法则计算得到最简结果，然后将已知等式代入计算即可求出值． 解:原式=[a2+b2+2ab-2b2-(a2-2ab+b2)]÷4b =[a2+b2+2ab-2b2-a2+2ab-b2]÷4b=[4ab-2b2]÷4b =a-b= (2...

    查看答案和解析>>

    同步练习册答案