
四张大小、质地均相同的卡片上分别标有数字1,2,3,4,现将标有数字的一面朝下扣在桌子上,从中随机抽取一张(不放回),再从桌子上剩下的3张中随机抽取第二张.
(1)用画树状图的方法,列出前后两次抽得的卡片上所标数字的所有可能情况;
(2)计算抽得的两张卡片上的数字之积为奇数的概率是多少?
(1) (2)P(积为奇数)= 【解析】(1)用树状图列举出2次不放回实验的所有可能情况即可; (2)看是奇数的情况占所有情况的多少即可.科目:初中数学 来源:2017-2018学年度鲍沟中学北师大版八年级数学上册 第一章 勾股定理 检测题 题型:单选题
已知Rt△ABC中,∠C=90°,若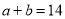 cm,
cm, 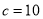 cm,则S△ABC为( ).
cm,则S△ABC为( ).
A. 24cm2 B. 36cm2 C. 48cm2 D. 60cm2
A 【解析】试题分析:根据直角三角形的勾股定理可得:==100,根据完全平方公式可得:,即+2ab=196,则ab=48,根据三角形的面积计算公式可得:S=ab=24.查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 第24章小结与复习 练习 题型:解答题
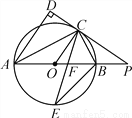
如图,AB 是⊙O 的直径,点C 是⊙O 上一点,AD 与过点C的切线垂直,垂足为 D,直线 DC 与AB 的延长线相交于点P,弦CE平分∠ACB,交AB 于点F,连接BE.
求证:(1)AC 平分∠DAB;
(2)△PCF 是等腰三角形.
查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 第24章小结与复习 练习 题型:单选题
如图,AB 是⊙O 的直径,点C 在⊙O 上,∠ABC=30°,AB=8,则BC 等于 ( )

A. 4; B. 4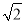 ; C. 4
; C. 4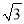 ; D. 8;
; D. 8;
查看答案和解析>>
科目:初中数学 来源:《概率的进一步认识》单元测试2 题型:解答题
一堆彩球有红、黄两种颜色,首先数出的50个球中有49个红球,以后每数出8个球中都有7个红球,一直数到最后8个球,正好数完,在已经数出的球中红球的数目不少于90%.
(1)这堆球的数目最多有多少个?
(2)在(1)的情况下,从这堆彩球中任取两个球,恰好为一红一黄的概率有多大?
(1)210个(2)0.18 【解析】试题分析:(1) 模了n次,利用已知列概率,令其大于等于0.9. (2)利用乘法原理. 试题解析: (1)210个.设每次摸8个球,共模了n次,则,∴ 当n=20时,共有210个球,∴这堆球的数目最多有210个. (2)在(1)的情况下,210个球中有21个黄球,189个红球,从中摸两个,恰为一黄一红的概率约为0.18.先取...查看答案和解析>>
科目:初中数学 来源:《概率的进一步认识》单元测试2 题型:单选题
一个均匀的立方体六个面上分别标有数1,2,3,4,5,6.如图是这个立方体表面的展开图.抛掷这个立方体,则朝上一面上的数恰好等于朝下一面上的数的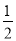 的概率是( )
的概率是( )
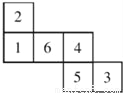
A. 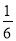 B.
B. 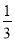 C.
C. 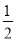 D.
D. 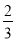
查看答案和解析>>
科目:初中数学 来源:《概率的进一步认识》单元测试2 题型:解答题
苏州市区某居民小区共有800户家庭,有关部门准备对该小区的自来水管网系统进行改造,为此,需了解该小区的自来水用水的情况.该部门通过随机抽样,调查了其中的30户家庭,已知这30户家庭共有87人.
(1)这30户家庭平均每户__________人;(精确到0.1人)
(2)这30户家庭的月用水量见下表:
月用水量( | 4 | 6 | 7 | 12 | 14 | 15 | 16 | 18 | 20 | 25 | 28 |
户数 | 1 | 2 | 3 | 3 | 2 | 5 | 3 | 4 | 4 | 2 | 1 |
求这30户家庭的人均日用水量;(一个月按30天计算,精确到0.001m3)
(3)根据上述数据,试估计该小区的日用水量?(精确到1m3)
(1)2.9(2)0.174m3(3)404m3 【解析】试题分析:(1)根据数据直接解答,用30户家庭的总用水量除以30; (2)先求出这30户家庭的月用水的总量,则人日用水量为用水总量÷(87×30). (3)用样本平均数根据总体平均数. (1)这30户家庭平均每户人数为87÷30=2.9人; (2)4×1+6×2+7×3+12×3+14×2+15×5+16×3+...查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 24.2.2直线和圆的位置关系(1)练习 题型:解答题
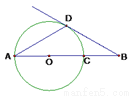
如图,线段AB经过圆心O,交⊙O于点A、C,?BAD=?B=30?,边BD交圆于点D.BD是⊙O的切线吗?为什么?
查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 23.1图形的旋转(2)测试 题型:解答题
观察下列图形,它可以看作是什么“基本图形”通过怎样的旋转而得到的?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com