练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，已知AB、CD、EF都与BD垂直，垂足分别是B、D、F，且AB=4，CD=12，那么EF的长是（　　）

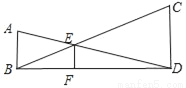
    A. 2 B. 2.5 C. 3 D. 2.8

    C 【解析】∵AB、CD、EF都与BD垂直， ∴AB∥EF∥CD， ∴△DEF∽△DAB，△BFE∽△BDC， ∴ ， ， ∴=1， ∵AB=4，CD=12， ∴EF=3， 故选C．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北京八十五中2017-2018学年上期期末八年级数学试卷 题型：单选题

    一个多边形每个外角都等于36°，则这个多边形是几边形（ ）

    A．7 B．8 C．9 D．10

    D 【解析】 试题分析：多边形的外角和是360°，又有多边形的每个外角都等于36°，所以可以求出多边形外角的个数，进而得到多边形的边数． 【解析】 这个多边形的边数是：=10．故答案是D．

    查看答案和解析>>

    科目：初中数学 来源：2017年甘肃省平凉市中考数学模拟试卷 题型：填空题

    如图，△ABC三边的中线AD、BE、CF的公共点为G，若S△ABC=12，则图中阴影部分的面积是______．

    4 【解析】

    查看答案和解析>>

    科目：初中数学 来源：2017年海南省定安县中考数学仿真试卷（二） 题型：解答题

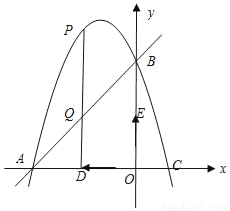
    如图，抛物线经过点A（﹣3，0）、B（0，3），C（1，0）．

    （1）求抛物线及直线AB的函数关系式；

    （2）有两动点D、E同时从O出发，以每秒1个单位长度的相同的速度分别沿线段OA、OB向A、B做匀速运动，过D作PD⊥OA分别交抛物线和直线AB于P、Q，设运动时间为t（0＜t＜3）．

    ①求线段PQ的长度的最大值；

    ②连接PE，当t为何值时，四边形DOEP是正方形；

    ③连接DE，在运动过程中，是否存在这样的t值，使PE=DE？若存在，请求出t的值；若不存在，请说明理由．

    （1）y=﹣x2﹣2x+3；y=x+3；（2）①当t=1时，PQ的长度有最大值，最大值为4；②当t为时，四边形DOEP是正方形；③存在．当t=时，PE=DE 【解析】试题分析：（1）已知了抛物线上的三个点的坐标和直线上两个点的坐标，直接利用待定系数法即可求出抛物线和直线的解析式；（2）①用t表示出线段PQ的长，利用二次函数的性质即可求解；②OE=OD=PD时，四边形四边形DOEP是正方形，由...

    查看答案和解析>>

    科目：初中数学 来源：2017年海南省定安县中考数学仿真试卷（二） 题型：填空题

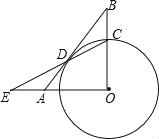
    如图，半径为3的⊙O与Rt△AOB的斜边AB切于点D，交OB于点C，连接CD交直线OA于点E，若∠B=30°，则线段AE的长为 ．

    【解析】 试题分析：要求AE的长，只要求出OA和OE的长即可，要求OA的长可以根据∠B=30°和OB的长求得，OE可以根据∠OCE和OC的长求得．连接OD，如图所示， 由已知可得，∠BOA=90°，OD=OC=3，∠B=30°，∠ODB=90°，∴BO=2OD=6，∠BOD=60°， ∴∠ODC=∠OCD=60°，AO=BOtan30°=6×=2，∵∠COE=90°，OC=3， ...

    查看答案和解析>>

    科目：初中数学 来源：2017年海南省定安县中考数学仿真试卷（二） 题型：单选题

    一块直角三角板和直尺按图3方式放置，若∠1=50°，则∠2=（　　）度．

    A. 40° B. 50° C. 130° D. 140°

    D 【解析】∵∠3=90°+∠1=90°+50°=140°， ∵直尺的两对边平行， ∴∠2=∠3=140°， 故选D．

    查看答案和解析>>

    科目：初中数学 来源：2017年海南省定安县中考数学仿真试卷（二） 题型：单选题

    2017的相反数是（　　）

    A. 2017 B. ﹣2017 C. D. ﹣

    B 【解析】试题解析：-2017的相反数是-（-2007）=2007. 故选A.

    查看答案和解析>>

    科目：初中数学 来源：重庆市校2018届九年级上学期期末模拟数学试卷 题型：单选题

    如图，⊙O的半径OD⊥弦AB于点C，连结AO并延长交⊙O于点E，连结EC．若AB=8，CD=2，则EC的长为（ ）

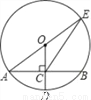
    A. 2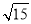 B. 8 C. 2 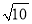D. 2

    C 【解析】连结BE，设⊙O的半径为R，由OD⊥AB，根据垂径定理得AC=BC=AB=4，在Rt△AOC中，OA=R，OC=R-CD=R-2，根据勾股定理得到（R-2）2+42=R2，解得R=5，则OC=3，由于OC为△ABE的中位线，则BE=2OC=6，再根据圆周角定理得到∠ABE=90°，然后在Rt△BCE中利用勾股定理可计算出CE． 【解析】 连结BE，设⊙O的半径为R，如图所...

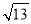
    查看答案和解析>>

    科目：初中数学 来源：江苏省东台市2017-2018学年上学期期末考试九年级数学试卷 题型：解答题

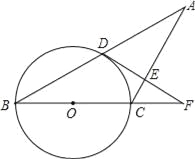
    已知：如图，△ABC中，AC=BC，以BC为直径的⊙O交AB于点D，过点D作DE⊥AC于点E，交BC的延长线于点F．

    求证：

    （1）AD=BD；

    （2）DF是⊙O的切线．

    （1）证法一：连结CD， ∵BC为⊙O的直径 ∴CD⊥AB ∵AC＝BC ∴AD＝BD． 证法二：连结CD， ∵BC为⊙O的直径 ∴∠ADC＝∠BDC＝90° ∵AC＝BC，CD＝CD ∴△ACD≌△BCD ∴AD＝BD （2）证法一：连结OD， ∵AD＝BD，OB＝OC ∴OD∥AC ∵DE⊥AC ∴DF⊥...

    查看答案和解析>>

    同步练习册答案