
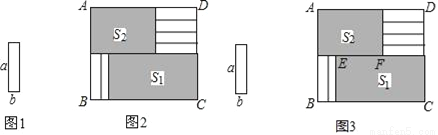
将6张小长方形纸片(如图1所示)按图2所示的方式不重叠的放在长方形ABCD内,未被覆盖的部分恰好分割为两个长方形,面积分别为S1和S2.已知小长方形纸片的长为a,宽为b,且a>b.当AB长度不变而BC变长时,将6张小长方形纸片还按照同样的方式放在新的长方形ABCD内,S1与S2的差总保持不变,求a,b满足的关系式.
(1)为解决上述问题,如图3,小明设EF=x,则可以表示出S1= ,S2= ;
(2)求a,b满足的关系式,写出推导过程.
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源:2017年河北省中考数学三模试卷 题型:填空题
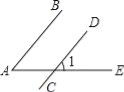
如图,平行线AB,CD被直线AE所截,∠1=50°,则∠A= .
查看答案和解析>>
科目:初中数学 来源:江苏省苏州市2017-2018学年七年级上期中试卷数学试卷 题型:单选题
用代数表示“ 的
的 倍与
倍与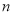 的差的平方”,正确的是( ).
的差的平方”,正确的是( ).
A. 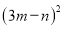 B.
B. 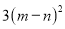 C.
C. 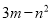 D.
D. 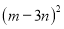
查看答案和解析>>
科目:初中数学 来源:2017年海南省中考数学模拟试卷 题型:单选题
如图,AB是⊙O的弦,AC是⊙O切线,A为切点,BC经过圆心.若∠B=20°,则∠C的大小等于( )
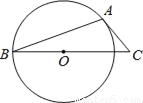
A. 20° B. 25° C. 40° D. 50°
D 【解析】试题解析:如图,连接OA, ∵AC是⊙O的切线, ∴∠OAC=90°, ∵OA=OB, ∴∠B=∠OAB=25°, ∴∠AOC=50°, ∴∠C=40°. 故选C.查看答案和解析>>
科目:初中数学 来源:2017年海南省中考数学模拟试卷 题型:单选题
已知长方形的面积为18x3y4+9xy2﹣27x2y2,长为9xy,则宽为( )
A. 2x2y3+y+3xy B. 2x2y2﹣2y+3xy C. 2x2y3+2y﹣3xy D. 2x2y3+y﹣3xy
D 【解析】试题解析:由题意得: 长方形的宽 故选D.查看答案和解析>>
科目:初中数学 来源:福建省2017-2018学年七年级上学期期中考试数学试卷 题型:解答题
化简:
(1)12x﹣20x+10x
(2)2(2a﹣3b)﹣3(2b﹣3a)
(1)2x (2)13a-12b 【解析】试题分下:(1)直接合并同类型即可,即把系数相加,字母和字母的指数不变; (2)先去括号,然后合并同类项,去括号时一是要注意不要漏乘括号内的项,二是注意括号前是“-”时,去掉括号和“-”后括号内各项的符号都要变号. 【解析】 (1)12x﹣20x+10x 原式=(12-20+10)x =2x (2)2(2a﹣3b)﹣3...查看答案和解析>>
科目:初中数学 来源:福建省2017-2018学年七年级上学期期中考试数学试卷 题型:填空题
如果-3(x+3)=6,那么x+3=-2根据是__________
等式性质2 【解析】∵把-3(x+3)=6的两边都除以-3可得x+3=-2, ∴该变形是根据等式的性质2.查看答案和解析>>
科目:初中数学 来源:山东省寿光市2017-2018学年七年级上期末模拟数学试卷 题型:解答题
画出数轴,把下列各数0,2,(﹣1)2 ,﹣|﹣3|,﹣2.5在数轴上分别用点A,B,C,D,E表示出来;按从小到大的顺序用“<”号将各数连接起来.
D<E<A<C<B. 【解析】试题分析:先在数轴上表示出各数,在从左到右用“<”连接起来即可. 试题解析:(﹣1)2 =1 , ﹣|﹣3|=-3, 如图所示, 故D<E<A<C<B. ,查看答案和解析>>
科目:初中数学 来源:2017年吉林省中考数学一诊试卷 题型:解答题
如图,抛物线y=ax2+bx+c交x轴于A(-4,0),B(1,0),交y轴于C点,且OC=2OB.
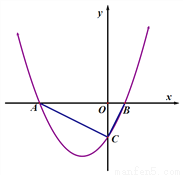
(1)求抛物线的解析式;
(2)在直线BC上找点D,使△ABD为以AB为腰的等腰三角形,求D点的坐标;
(3)在抛物线上是否存在异于B的点P,过P点作PQ⊥AC于Q,使△APQ与△ABC相似?若存在,请求出P点坐标;若不存在,请说明理由.
(1)抛物线的解析式为; (2)满足条件的D点有D1 ,D2,D3(?1,?4); (3)满足条件的点P有P和P′ 【解析】【解析】 (1)依题意得, ,解得, , ∴抛物线的解析式为; (2)①以AD为底时,AB=BD, 设直线BC的解析式为y=kx+b,则, ∴直线BC的解析式为y=2x?2, 设D(x,2x?2),由(2x?2)2+(1?x)...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com