
解不等式组 ,并将它的解集在数轴上表示出来.
,并将它的解集在数轴上表示出来.
科目:初中数学 来源:2017年河北省中考数学模拟试卷 题型:填空题
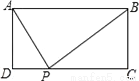
如图,矩形ABCD中,AD=2,AB=5,P为CD边上的动点,当△ADP与△BCP相似时,DP=__.
查看答案和解析>>
科目:初中数学 来源:山东省诸城市2017-2018学年七年级上期末模拟数学试卷 题型:单选题
为创建园林城市,盐城市将对城区主干道进行绿化,计划把某一段公路的一侧全部栽上桂花树,要求路的两端各栽一棵,并且每两棵树的间隔相等.如果每隔6米栽1棵,则树苗缺22棵;如果每隔7米栽1棵,则树苗正好用完.设原有树苗x棵,则根据题意列出方程正确的是( )
A. 6(x+22)=7(x-1) B. 6(x+22-1)=7(x-1)
C. 6(x+22-1)=7x D. 6(x+22)=7x
B 【解析】试题分析:设原有树苗x棵,根据首、尾两端均栽上树,每间隔6米栽一棵,则缺少22棵,可知这一段公路长为6(x+22﹣1);若每隔7米栽1棵,则树苗正好用完,可知这一段公路长又可以表示为7(x﹣1),根据公路的长度不变列出方程即可. 【解析】 设原有树苗x棵,由题意得 6(x+22﹣1)=7(x﹣1). 故选:B.查看答案和解析>>
科目:初中数学 来源:2017年湖南省郴州市汝城县濠头学校中考数学模拟试卷 题型:单选题
一个几何体的三视图如图所示,则这个几何体是( )
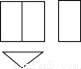
A. 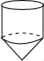 B.
B. 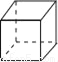 C.
C. 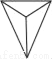 D.
D. 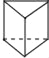
查看答案和解析>>
科目:初中数学 来源:2017年天津市中考数学模拟试卷(1) 题型:解答题
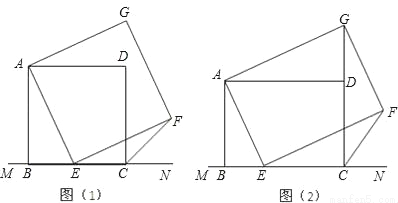
如图(1),已知正方形ABCD在直线MN的上方,BC在直线MN上,E是BC上一点,以AE为边在直线MN的上方作正方形AEFG.
(1)连接GD,求证:△ADG≌△ABE;
(2)连接FC,观察并猜测∠FCN的度数,并说明理由;
(3)如图(2),将图(1)中正方形ABCD改为矩形ABCD,AB=a,BC=b(a、b为常数),E是线段BC上一动点(不含端点B、C),以AE为边在直线MN的上方作矩形AEFG,使顶点G恰好落在射线CD上.判断当点E由B向C运动时,∠FCN的大小是否总保持不变?若∠FCN的大小不变,请用含a、b的代数式表示tan∠FCN的值;若∠FCN的大小发生改变,请举例说明.
查看答案和解析>>
科目:初中数学 来源:2017年天津市中考数学模拟试卷(1) 题型:单选题
若(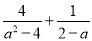 )•w=1,则w=( )
)•w=1,则w=( )
A. a+2(a≠﹣2) B. ﹣a+2(a≠2) C. a﹣2(a≠2) D. ﹣a﹣2(a≠﹣2)
D 【解析】∵=== 又∵()•w=1, ∴w=?a?2. 故选:D.查看答案和解析>>
科目:初中数学 来源:2017年安徽省中考数学模拟试卷 题型:填空题
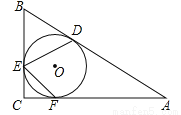
如图,在Rt△ABC中,∠C=90°,∠B=70°,△ABC的内切圆⊙O与边AB、BC、CA分别相切于点D、E、F,则∠DEF的度数为 °.
查看答案和解析>>
科目:初中数学 来源:江苏省徐州市区联校2017-2018学年七年级上学期期中联考数学试卷 题型:解答题
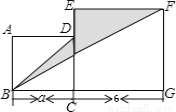
如图,正方形ABCD和正方形ECGF的边长分别为a和6,
(1) 写出表示阴影部分面积的代数式(结果要求化简);
(2) 求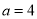 时,阴影部分的面积.
时,阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com