
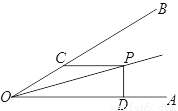
如图,在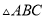 中,
中, 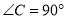 ,请你用直尺和圆规在边
,请你用直尺和圆规在边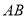 上确定一点
上确定一点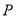 使
使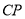 将
将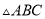 分成两个等腰三角形.(尺规作图,要求保留作图痕迹,不必写出作法).
分成两个等腰三角形.(尺规作图,要求保留作图痕迹,不必写出作法).

 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源:湖南省耒阳市冠湘学校2018届九年级上学期第二次段考(期中)考试数学试卷 题型:解答题
计算:
(1) 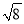 ﹣|﹣
﹣|﹣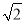 |+(﹣π)0﹣(﹣1)2015 .
|+(﹣π)0﹣(﹣1)2015 .
(2) 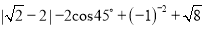 .
.
查看答案和解析>>
科目:初中数学 来源:黑龙江省大庆市(五四制)2017-2018学年七年级上学期期中考试数学试卷 题型:单选题
∠A的余角与∠A的补角互为补角,那么2∠A是( )
A. 直角 B. 锐角 C. 钝角 D. 以上三种都有可能
A 【解析】设∠A=x°,则它的余角为(90°?x),补角为(180°?x), 依题意,得(90°?x)+(180°?x)=180° 解得x=45°. ∴2∠A=90°,即是直角。 故选:A.查看答案和解析>>
科目:初中数学 来源:初一数学第一学期5.5应用一元一次方程-“希望工程”义演 同步练习 题型:填空题
甲、乙两人练习赛跑,若甲让乙先跑10米,则甲跑5秒种就能追上乙.若甲让乙先跑2秒钟,则甲跑4秒种就能追上乙,则甲每秒跑____米,乙每秒跑____米.
6 4 【解析】设甲每秒跑x米,则乙每秒跑x?=(x?2)米, 根据题意得:4x=6(x?2), 去括号得:4x=6x?12, 解得:x=6, 则甲每秒跑6米,乙每秒跑4米。 故答案为:6;4.查看答案和解析>>
科目:初中数学 来源:初一数学第一学期5.5应用一元一次方程-“希望工程”义演 同步练习 题型:单选题
A、B两地相距900千米,甲乙两车分别从A、B两地同时出发,相向而行,已知甲车的速度为110千米/时,乙车的速度为90千米/时,则当两车相距100千米时,甲车行驶的时间是( )
A. 4小时 B. 4.5小时 C. 5小时 D. 4小时或5小时
D 【解析】设当两车相距100千米时,甲车行驶的时间为x小时, 根据题意得:900?(110+90)x=100或(110+90)x?900=100, 解得:x=4或x=5. 故选D.查看答案和解析>>
科目:初中数学 来源:陕西省2016-2017学年八年级下学期期末考试数学试卷 题型:填空题
如图, 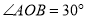 ,
, 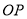 是
是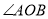 的平分线,
的平分线, 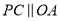 ,
, 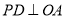 ,若
,若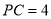 ,则
,则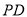 的值为__________.
的值为__________.
查看答案和解析>>
科目:初中数学 来源:陕西省2016-2017学年八年级下学期期末考试数学试卷 题型:单选题
如图,平行四边形 中,
中, 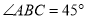 ,
,  、
、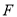 分别在
分别在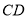 和
和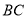 的延长线上,
的延长线上, 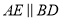 ,
, 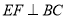 ,
, 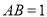 ,则
,则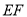 的长是( ).
的长是( ).

A. 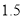 B.
B. 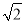 C.
C. 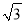 D.
D. 
查看答案和解析>>
科目:初中数学 来源:数学人教版八年级上册第11章第二节与三角形有关的角第一课时同步练习 题型:填空题
如图,已知,AB∥CD,直线EF分别交AB,CD于E、F,点G在直线EF上,GH⊥AB,若∠EGH=32°,则∠DFE的度数为____________.
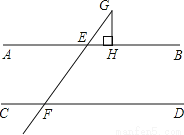
查看答案和解析>>
科目:初中数学 来源:天津武清区数学试卷八年级《11.3 多边形及其内角和》同步测试 题型:单选题
一个多边形的内角和是它的外角和的2倍,则这个多边形是( )
A. 四边形 B. 五边形 C. 六边形 D. 七边形
C 【解析】【解析】 设多边形边数为n,根据题意,得:(n﹣2)•180=720,解得:n=6,故选C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com