
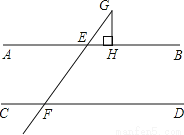
如图,已知,AB∥CD,直线EF分别交AB,CD于E、F,点G在直线EF上,GH⊥AB,若∠EGH=32°,则∠DFE的度数为____________.
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源:黑龙江省大庆市(五四制)2017-2018学年七年级上学期期中考试数学试卷 题型:填空题
计算:am•a3•________=a3m+2.
【解析】根据题意列得:a3m+2÷(am?a3)=a3m+2÷am+3=a2m?1. 故答案为:a2m?1查看答案和解析>>
科目:初中数学 来源:陕西省2016-2017学年八年级下学期期末考试数学试卷 题型:解答题
如图,在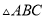 中,
中, 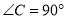 ,请你用直尺和圆规在边
,请你用直尺和圆规在边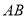 上确定一点
上确定一点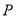 使
使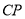 将
将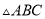 分成两个等腰三角形.(尺规作图,要求保留作图痕迹,不必写出作法).
分成两个等腰三角形.(尺规作图,要求保留作图痕迹,不必写出作法).

查看答案和解析>>
科目:初中数学 来源:陕西省2016-2017学年八年级下学期期末考试数学试卷 题型:单选题
下列因式分解正确的是( ).
A. 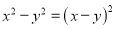 B.
B. 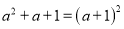 C.
C. 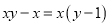 D.
D. 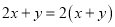
查看答案和解析>>
科目:初中数学 来源:数学人教版八年级上册第11章第二节与三角形有关的角第一课时同步练习 题型:填空题
小明在学习三角形内角和定理时,自己做了如下推理过程,请你帮他补充完整.
已知:如图,△ABC中,∠A、∠B、∠C是它的三个内角,那么这三个内角的和等于多少?为什么?

【解析】
∠A+∠B+∠C=180°
理由:作∠ACD=∠A,并延长BC到E
∠1=∠A(已作)
∴AB∥CD (_________________________)
∴∠B=_____(_________________________)
而∠ACB+∠1+∠2=180°
∴∠ACB+_____+_____=180°(等量代换)
内错角相等,两直线平行;∠2;两直线平行,同位角相等;∠B;∠A. 【解析】试题分析:作∠ACD=∠A,并延长BC到E.利用平行线的判定推知AB∥CD,然后根据平行线的性质可知∠B=∠2;最后由等量代换证得∠ACB+∠B+∠A=180°. 试题解析:【解析】 ∠A+∠B+∠C=180°. 理由:作∠ACD=∠A,并延长BC到E ∠1=∠A(已作) ∴AB∥CD (内...查看答案和解析>>
科目:初中数学 来源:数学人教版八年级上册第11章第二节与三角形有关的角第一课时同步练习 题型:单选题
如图,AE是△ABC的角平分线,AD⊥BC于点D,若∠BAC=128°,∠C=36°,则∠DAE= °.
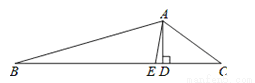
查看答案和解析>>
科目:初中数学 来源:数学人教版八年级上册第11章第二节与三角形有关的角第一课时同步练习 题型:单选题
三角形的三个内角( )
A、至少有两个锐角 B、至少有一个直角
C、至多有两个钝角 D、至少有一个钝角
A 【解析】根据三角形的内角和是180°判断即可. 【解析】 根据三角形的内角和是180°,知:三个内角可以都是60°,排除B; 三个内角可以都是锐角,排除C和D; 三角形的三个内角中至少有两个锐角,不可能有两个钝角或两个直角. 故选A. 考查了三角形的内角和定理:三角形的三个内角和是180°.查看答案和解析>>
科目:初中数学 来源:天津武清区数学试卷八年级《11.3 多边形及其内角和》同步测试 题型:解答题
一个多边形的内角和与某一个外角的度数总和为1350°,求这个多边形的边数.
九 【解析】试题分析:根据多边形的内角和公式可知180×7=1260<1350<180×8=1440,所以一个外角只能为1350﹣1260=90,由此得出多边形的边数为7+2=9求得问题. 试题解析:【解析】 设这个多边形的边数为n,180×(n﹣2)=1350﹣,180×7=1260<1350<180×8=1440,所以一个外角只能为1350﹣1260=90,由此得出多边形的边数为...查看答案和解析>>
科目:初中数学 来源:山东省聊城市2018届九年级上学期期中考试数学试卷 题型:解答题
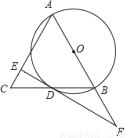
如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作EF⊥AC于点E,交AB的延长线于点F.
(1)判断直线DE与⊙O的位置关系,并说明理由;
(2)如果AB=5,BC=6,求DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com