
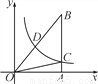
如图,已知双曲线y=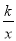 (k>0)与直角三角形OAB的直角边AB相交于点C,且BC=3AC,若△OBC的面积为3,则k=_________.
(k>0)与直角三角形OAB的直角边AB相交于点C,且BC=3AC,若△OBC的面积为3,则k=_________.
科目:初中数学 来源:浙江省宁波市东钱湖九校2017-2018学年七年级上册数学期中联考试卷 题型:单选题
用12m长的铝合金做成一个长方形的窗框(如图),设长方形窗框横条的长度为x(m),则长方形窗框的面积为( )
A. x(12-x) m2 B. x(6-x) m2 C. x(6-1.5x) m2 D. x(6-2x) m2
C 【解析】试题解析:长方形窗框横条的长度为则宽是: 故长方形窗框的面积: 故选C.查看答案和解析>>
科目:初中数学 来源:广东省2017-2018学年八年级上学期第二次统测数学试卷 题型:解答题
计算:(a-b)(a+b)+2ab3÷ab
【解析】试题分析:按运算顺序先利用平方差公式进行乘法运算,同时进行后面的除法运算,然后再合并同类项即可. 试题解析:原式==.查看答案和解析>>
科目:初中数学 来源:广东省2017-2018学年八年级上学期第二次统测数学试卷 题型:单选题
以下列各组线段为边,能组成三角形的是( )
A. 2 cm ,3 cm,5 cm B. 3 cm,3 cm,6 cm
C. 5 cm,8 cm,2 cm D. 4 cm,5 cm,6 cm
D 【解析】A选项:2+3=5,不能组成三角形; B选项:3+3=6,不能组成三角形; C选项:2+5<8,不能够组成三角形; D选项:4+5>6,能组成三角形. 故选D.查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学下册(华师大版):期末检测1 题型:解答题
(本题8分)射击队为从甲、乙两名运动员中选拔一人参加比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 平均成绩 | 中位数 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 | 9 | ① |
乙 | 10 | 7 | 10 | 10 | 9 | 8 | ② | 9.5 |
(1)完成表中填空① ;② ;
(2)请计算甲六次测试成绩的方差;
(3)若乙六次测试成绩方差为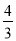 ,你认为推荐谁参加比赛更合适,请说明理由.
,你认为推荐谁参加比赛更合适,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学下册(华师大版):期末检测1 题型:填空题
计算:(-3)0+(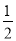 )-2-
)-2-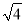 的结果是_______.
的结果是_______.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学下册(华师大版):期末检测1 题型:单选题
下列分式是最简分式的是( )
A.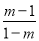 B.
B.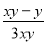 C.
C.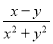 D.
D.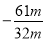
查看答案和解析>>
科目:初中数学 来源:广东省2018届九年级上学期学业检测(二)数学试卷 题型:填空题
在平面直角坐标系中,点P(1,-5)关于原点对称点P′的坐标是。
(-1,5). 【解析】 试题分析:点P(1,-5)关于原点对称的点的坐标是(-1,5).故答案为:(-1,5).查看答案和解析>>
科目:初中数学 来源:北京海淀区2017-2018学年初二第一学期数学期末试卷 题型:解答题
如图,A,B,C,D是同一条直线上的点,AC=BD,AE∥DF,∠1=∠2.求证:BE = CF.
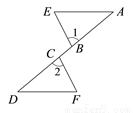
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com