练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    解方程：x2﹣2x﹣2=0．

    x1=1+，x2=1﹣． 【解析】试题分析：把常数项2移项后，应该在左右两边同时加上一次项系数﹣2的一半的平方． 试题解析：x2﹣2x﹣2=0 移项，得 x2﹣2x=2， 配方，得 x2﹣2x+1=2+1，即（x﹣1）2=3， 开方，得 x﹣1=±． 解得x1=1+，x2=1﹣．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：重庆市校2017-2018学年七年级上学期第二阶段考试数学试卷 题型：填空题

    比较大小：（1）34______43； （2）______.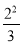

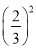    ＞ ＞ 【解析】（1）34=81，43=64，81>64，所以34>43； （2） ，所以>， 故答案为：(1). ＞；(2). ＞.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年七年级数学下册（人教版）期末检测题 题型：解答题

    如图，若AB∥CD，∠1＝∠2，∠3＝∠4，AD与BC平行吗？为什么？

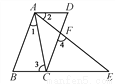
    AD∥BC 【解析】试题分析：由两直线平行，同位角相等可得，利用三角形的内角和为180°，证得 运用内错角相等，两直线平行易证AD与BC平行． 试题解析：AD∥BC. 理由如下：∵AB∥CD， ∴∠FCE=∠B， 即∠E=∠2， ∴AD∥BC.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年七年级数学下册（人教版）期末检测题 题型：单选题

    代入法解方程组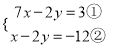有以下步骤：(1)由①，得2y＝7x－3③；(2)把③代入①，得7x－7x－3＝3；(3)整理，得3＝3；(4)∴x可取一切有理数，原方程组有无数组解．以上解法造成错误步骤是(　 　)

    A. 第(1)步 B. 第(2)步 C. 第(3)步 D. 第(4)步

    B 【解析】试题解析：错的是第步，应该将③代入②. 故选B.

    查看答案和解析>>

    科目：初中数学 来源：湖北省武汉市洪山区2018届九年级（上）期中数学试卷 题型：解答题

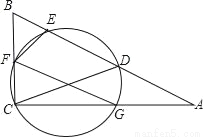
    如图，D为Rt△ABC斜边AB上一点，以CD为直径的圆分别交△ABC三边于E、F、G三点，连接FE，FG．

    （1）求证：∠EFG=∠B；

    （2）若AC=2BC=4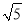，D为AE的中点，求FG的长．

    （1）证明见解析；（2）4 【解析】试题分析：（1）连接EC，则∠AEC=90°，由同角的余角相等即可得出∠B=∠ECA，再根据圆周角定理即可得出∠ECA=∠EFG，由此即可证出∠EFG=∠B； （2）由AC、BC的长度利用勾股定理即可求出AB的长度，结合面积法即可得出CE的长度，由正切即可得出AE的长度，再利用勾股定理可求出CD的长度，连接FD、DG，由矩形的判定定理即可证出四边形F...

    查看答案和解析>>

    科目：初中数学 来源：湖北省武汉市洪山区2018届九年级（上）期中数学试卷 题型：填空题

    一次会议上，每两个参加会议的人都相互握一次手，有人统计一共握了36次手，设到会的人数为x人，则根据题意列方程为_____．

    x（x﹣1）=36 【解析】试题解析：设到会的人数为x人，则每个人握手（x﹣1）次， 由题意得， x（x﹣1）=36， 故答案是： x（x﹣1）=36．

    查看答案和解析>>

    科目：初中数学 来源：湖北省武汉市洪山区2018届九年级（上）期中数学试卷 题型：单选题

    如图，在平面直角坐标系xOy中，△ABC顶点的横、纵坐标都是整数．若将△ABC以某点为旋转中心，顺时针旋转90°得到△DEF，则旋转中心的坐标是（　　）

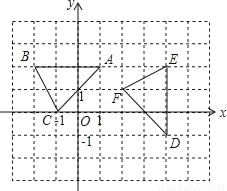
    A. （0，0） B. （1，0） C. （1，﹣1） D. （2.5，0.5）

    C 【解析】试题解析：∵将△ABC以某点为旋转中心，顺时针旋转90°得到△DEF， ∴点A的对应点为点D，点B的对应点为点E， 作线段AD和BE的垂直平分线，它们的交点为P（1，﹣1）， ∴旋转中心的坐标为（1，﹣1）． 故选C．

    查看答案和解析>>

    科目：初中数学 来源：甘肃省平凉市崆峒区2017-2018学年度第一学期期末数学试卷及答案 题型：填空题

    如图，AB=12，C为线段AB的中点，点D在线段AC上，且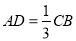,则BD的长度为 。

    10 【解析】【解析】 ∵AB=12，C为AB的中点，∴AC=BC=6．∵AD：CB=1：3，∴AD=2，∴DC=6-2=4，∴BD=DC+BC=4+6=10．故答案为：10．

    查看答案和解析>>

    科目：初中数学 来源：重庆市2018届2017年秋期期末冲刺卷 题型：解答题

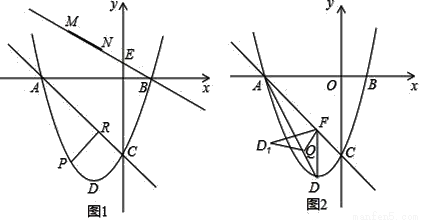
    如图1，已知抛物线y=x2+2x﹣3与x轴相交于A，B两点，与y轴交于点C，D为顶点．

    （1）求直线AC的解析式和顶点D的坐标；

    （2）已知E（0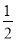， ），点P是直线AC下方的抛物线上一动点，作PR⊥AC于点R，当PR最大时，有一条长为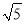的线段MN（点M在点N的左侧）在直线BE上移动，首尾顺次连接A、M、N、P构成四边形AMNP，请求出四边形AMNP的周长最小时点N的坐标；

    （3）如图2，过点D作DF∥y轴交直线AC于点F，连接AD，Q点是线段AD上一动点，将△DFQ沿直线FQ折叠至△D1FQ，是否存在点Q使得△D1FQ与△AFQ重叠部分的图形是直角三角形？若存在，请求出AQ的长；若不存在，请说明理由．

    （1）直线AC的解析式为y=﹣x﹣3，点D坐标（﹣1，﹣4）；（2）N（0， ）；（3）AQ的长为1+或或． 【解析】试题分析：（1）分别令x=0，y=0，可得A、B、C三点坐标，利用待定系数法设直线AC的解析式为y=kx+b，转化为解方程组即可． （2）如图1中，设P（m，m2+2m-3），由题意，当PR最大时，△ACP的面积最大，即四边形APCO的面积最大，因为S四边形APCO=S...

    查看答案和解析>>

    同步练习册答案