练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    若两个相似三角形的周长比为2：3，则它们的面积比是_________.

    4∶9 【解析】试题解析：∵两个相似三角形的周长比为2：3， ∴这两个相似三角形的相似比为2：3， ∴它们的面积比是4：9．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北师大版七年级数学下册 第二章 相交线与平行线 2.2 探索直线平行的条件 同位角及平行公理 同步课堂练习题 题型：填空题

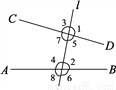
    如图，具有∠1与____这样位置关系的角称为同位角，图中的同位角还有∠3与____，∠5与____，∠7与____.

    ∠2 ∠4 ∠6 ∠8 【解析】根据同位角的判定：如图，具有∠1与∠2这样位置关系的角称为同位角， 图中的同位角还有∠3与∠4，∠5与∠6，∠7与∠8 故答案为： ∠2 , ∠4 , ∠6 ,∠8 .

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下2.2.1 用“同位角、第三直线”判定平行线 同步练习 题型：解答题

    如图,已知直线a,b,c,d,e,且∠1=∠2,∠3=∠4,则a与c平行吗?为什么?

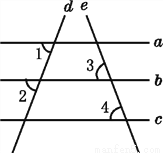
    解:a与c平行.

    理由:因为∠1=∠2(_________________), 

    所以a∥b(_________________). 

    因为∠3=∠4(_________________), 

    所以b∥c(_________________). 

    所以a∥c(_________________).

    已知;同位角相等,两直线平行;已知;同位角相等,两直线平行;平行于同一条直线的两条直线平行 【解析】由已知∠1=∠2，根据内错角相等，两直线平行可知a∥b，由∠3=∠4，根据同旁内角互补，两直线平行可知b∥c，根据如果两条直线都与第三条直线平行那么这两条直线平行得出结论a∥c． 故答案为：已知;同位角相等,两直线平行;已知;同位角相等,两直线平行;平行于同一条直线的两条直线平行.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年九年级数学北师大版上册 全册综合测试卷1 题型：解答题

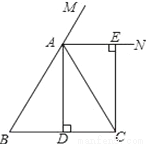
    已知：如图，在△ABC中，AB=AC，AD⊥BC，垂足为点D，AN是△ABC外角∠CAM的平分线，CE⊥AN，垂足为点E，

    （1）求证：四边形ADCE为矩形；

    （2）当△ABC满足什么条件时，四边形ADCE是一个正方形？并给出证明．

    （1）证明见解析；（2）当△ABC满足∠BAC=90°时，四边形ADCE是一个正方形，理由见解析. 【解析】试题分析：（1）求出∠BAD=∠DAC，∠MAE=∠CAE，求出∠DAE的度数，求出∠AEC=∠ADC=∠EAD=90°，根据矩形的判定判断即可； （2）求出AD=DC，得出∠ACD=∠DAC=45°，求出∠BAC=90°，即可求出答案． 试题解析：（1）证明：∵在△ABC...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年九年级数学北师大版上册 全册综合测试卷1 题型：填空题

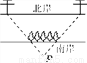
    如图，一条河的两岸有一段是平行的，在河的南岸边每隔5米有一棵树，在北岸边每隔50米有一根电线杆，小丽站在离岸边15米的点P处看北岸，发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住，并且这两棵树之间还有三棵树，则河的宽度为_______米．

    22.5 【解析】试题分析：根据题意，河两岸平行，故可根据平行线分线段成比例来解决问题，列出方程，求解即可． 【解析】 如图，设河宽为h， ∵AB∥CD 由平行线分线段成比例定理得：=， 解得：h=22.5， ∴河宽为22.5米． 故答案为：22.5．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年九年级数学北师大版上册 全册综合测试卷1 题型：单选题

    如图，在△ABC中，DE∥BC，AD=6，DB=3，AE=4，则EC的长为（　　）

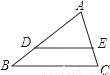
    A. 1 B. 2 C. 3 D. 4

    B 【解析】试题分析：根据平行线分线段成比例可得，代入计算可得： ，即可解EC=2， 故选：B．

    查看答案和解析>>

    科目：初中数学 来源：江苏省张家港市2017-2018学年第一学期初三数学期末考试试卷 题型：解答题

    如图，已知一条直线过点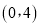，且与抛物线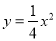交于A、B两点，其中点A的横坐标是-2.

    ⑴求这条直线的函数关系式及点B的坐标 ；

    ⑵在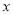轴上是否存在点C,使得?ABC是直角三角形？若存在，求出点C的坐标，若不存在，请说明理由；

    ⑶.过线段AB上一点P,作PM∥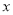轴，交抛物线于点M,点M在第一象限；点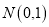，当点M的横坐标为何值时，MN+3MP的长度最大？最大值是多少？

    （1）点B的坐标为（8，16）；（2）点C的坐标为（，0），（0，0），（6，0），（32，0）；（3）当M的横坐标为6时，MN+3PM的长度的最大值是18. 【解析】试题分析：(1)、根据点A在二次函数上求出点A的坐标，然后利用待定系数法求出一次函数的解析式，根据一次函数和二次函数的交点坐标求出求出点B的坐标；(2)、根据点A和点B的坐标求出的值，设点C的坐标为(m，0)，然后分别求出和的...

    查看答案和解析>>

    科目：初中数学 来源：江苏省张家港市2017-2018学年第一学期初三数学期末考试试卷 题型：单选题

    如图，PA、PB切⊙O于A、B两点，CD切⊙O于点E，交PA，PB于C、D，若⊙O的半径为r，△PCD的周长等于3r，则tan∠APB的值是（ ）

    A． B． C． D．

    B． 【解析】 试题分析：如答图，连接PO，AO，取AO中点G，连接AG，过点A作AH⊥PO于点H， ∵PA、PB切⊙O于A、B两点，CD切⊙O于点E， ∴PA=PB，CA=CE，DB=DE，∠APO=∠BPO，∠OAP=90º. ∵△PCD的周长等于3r，∴PA=PB=. ∵⊙O的半径为r，∴在Rt△APO中，由勾股定理得. ∴. ∵∠OHA=∠OAP=...

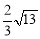
    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级下册数学 第二章 相交线与平行线 单元检测卷 题型：填空题

    一个正方体中有一条棱是a，与a平行棱长有________ 条，与a垂直并相交的棱长有________ 条．

    3； 4. 【解析】根据长方体的特征，12条棱分别互相平行的有3组，每组4条棱的长度相等且平行，由此可知：与a平行的棱有3条，与a相交并垂直的棱有4条． 【解析】 由分析得：与a平行的棱有3条，与a相交并垂直的棱有4条。 故答案为：3，4.

    查看答案和解析>>

    同步练习册答案