
��������:
����֪��ABC����ƽ������һ��P��ʹ���������ε���������ľ���֮����С��
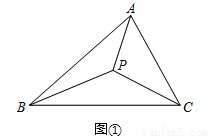
��������Ƿ�����ѧ�ҷ���1640��ǰ�������������ѧ�������������ģ�����ĵ㱻���dz�Ϊ�������㡱��
��ͼ�٣�����ABC�����ڽǾ�С��120��ʱ��������P�ڡ�ABC�ڲ�����ʱ��APB����BPC����CPA��120�㣬��ʱ��PA��PB��PC��ֵ��С��
������⣺
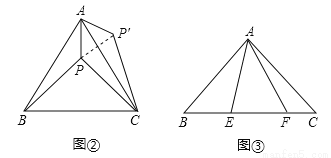
��1����ͼ�ڣ��ȱߡ�ABC����һ��P������P������A��B��C�ľ���ֱ�Ϊ3��4��5�����APB�Ķ�����
Ϊ�˽�����⣬���ǿ��Խ���ABP�ƶ���A��ת����ACP�䴦����ʱ��ACP��ա�ABP�������Ϳ���������ת�任���������߶�PA��PB��PCת����һ���������У��Ӷ������APB=�� ����
�������ã�
��2���������õڣ�1����Ľ��˼�뷽��������������⣺
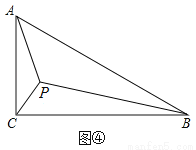
��ͼ�ۣ���ABC�У���CAB=90�㣬AB=AC��E��FΪBC�ϵĵ㣬�ҡ�EAF=45�㣬�ж�BE��EF��FC֮���������ϵ��֤����
����������
��3����ͼ�ܣ���Rt��ABC�У���C=90�㣬AC=1����ABC=30�㣬��PΪRt��ABC�ķ����㣬
����AP��BP��CP����PA+PB+PC��ֵ��

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ2017-2018ѧ����꼶��ѧ����ĩ�Ծ���ѧ ���ͣ������
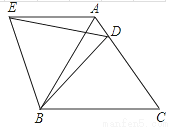
��ͼ���ڵȱߡ�ABC�У�D�DZ�AC��һ�㣬����BD������BCD�Ƶ�B��ʱ����ת60��õ���BAE������ED����BC=10��BD=9�����AED���ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ̩����������2017-2018ѧ����꼶��ѧ����ĩ���������ѧ�Ծ� ���ͣ���ѡ��
��ͼ����A�Ƿ���������y=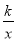 ��x��0����ͼ���ϵ�һ�㣬����A��ƽ���ı���ABCD��ʹ��B��C��x���ϣ���D��y���ϣ���֪ƽ���ı���ABCD�����Ϊ6����k��ֵΪ��������
��x��0����ͼ���ϵ�һ�㣬����A��ƽ���ı���ABCD��ʹ��B��C��x���ϣ���D��y���ϣ���֪ƽ���ı���ABCD�����Ϊ6����k��ֵΪ��������
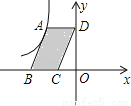
A. 6 B. 3 C. ��6 D. ��3
C ����������AE��BC��E����ͼ�� ���ı���ABCDΪƽ���ı��Σ� ��AD��x�ᣬ ���ı���ADOEΪ���Σ� ��Sƽ���ı���ABCD=S����ADOE�� ��S����ADOE=|?k|�� ��|?k|=6�� ��k<0����k<0�� ��k=?6. ��ѡ��C.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������������2017-2018ѧ����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
һ������ε��ڽǺ���1800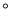 ������������____ ���Σ�
������������____ ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������������2017-2018ѧ����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ���ѡ��
��ͼ���߶�AC��BD���ڵ�0����OA=OC��������һ��������ʹ��AOB�ա�COD�����������( )
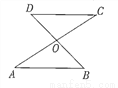
A. AC=BD B. OD=OC C. ��A=��C D. OA=OB
C �����������������A������AC=BD�����ж���OAB�ա�COD���ʴ�ѡ����� B������OD=OC�����ж���OAB�ա�COD���ʴ�ѡ����� C�����ӡ�A=��C��������ASA�ж���OAB�ա�COD���ʴ�ѡ����ȷ�� D������AO=BO�������ж���OAB�ա�COD���ʴ�ѡ����� ��ѡC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������������2017-2018ѧ����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
��ֱ������ϵ�л���һ�κ���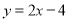 ��ͼ������������⣺
��ͼ������������⣺
��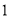 ���˺���ͼ����������Χ�ɵ������ε������______��
���˺���ͼ����������Χ�ɵ������ε������______��
��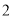 ���۲�ͼ��
���۲�ͼ��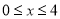 ʱ��y��ȡֵ��Χ��______��
ʱ��y��ȡֵ��Χ��______��
��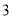 ����ֱ��
����ֱ��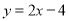 ƽ�ƺ���
ƽ�ƺ���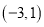 ����ƽ�ƺ��ֱ�ߵĺ�������ʽ��
����ƽ�ƺ��ֱ�ߵĺ�������ʽ��
����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������������2017-2018ѧ����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
��֪a��b��c�ǡ�ABC�����߳���c=5��a��b�����ϵʽ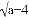 +��b��3��2=0�����ABC����״Ϊ_______�����Σ�
+��b��3��2=0�����ABC����״Ϊ_______�����Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017-2018ѧ�����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
ij�е������ŶԾ����õ簴���շѣ������£�
�� �õ粻����100�ȵģ�ÿ���շ�0.5Ԫ��
�� �õ糬��100�ȵģ���������ÿ���շ�0.8Ԫ��
��1��С����1�·��õ�140�ȣ�Ӧ�ɷ�________Ԫ��
��2��С����2�·��õ�ƽ��ÿ��0.65Ԫ���ʣ�����2�·����˶��ٶȵ磿
��1��82Ԫ����2��200. �������������������1���ܵ��=100��0.5+���õ����-100����0.8���������ݼ��ɵó����ۣ� ��2����С����2�·����˶ȵ磬��0.65>0.5�ɵó��������ܵ��=100��0.5+���õ����-100����0.8���ɵó����ڵ�һԪһ�η��̣���֮���ɵó����ۣ� �����������1�� (Ԫ). ��2����С�������˶ȵ磬 ��������ã� ��ã� ...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�����������2017-2018ѧ�����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ���ѡ��
�۲�ͼ�Σ�����˵����ȷ�ĸ����ǣ� ��
��1��ֱ��BA��ֱ��AB��ͬһ��ֱ�ߣ�
��2��AB+BD��AD��
��3������AC������AD��ͬһ�����ߣ�
��4������ֱ�������ཻʱ��һ������������
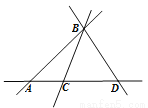
A. 1�� B. 2�� C. 3�� D. 4��
C �������������������1��ֱ��BA��ֱ��AB��ͬһ��ֱ�ߣ���ȷ�� ��2��AB+BD��AD����ȷ ��3������AC������AD��ͬһ�����ߣ���ȷ�� ��4������ֱ�������ཻʱ��һ�����������㣬��������һ�����ʲ���ȷ�� ��3��˵����ȷ�� ��ѡC���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com