
瑞士中学教师巴尔末成功的从光谱数据:  ,
,  ,
,  ,
, 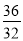 ,……中得到巴尔末公式,从而打开光谱奥妙的大门。请你根据以上光谱数据的规律写出它的第七个数据_______________.
,……中得到巴尔末公式,从而打开光谱奥妙的大门。请你根据以上光谱数据的规律写出它的第七个数据_______________.
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案科目:初中数学 来源:江苏省东台市第三教育联盟2017-2018学年度第一学期第三次阶段检测七年级数学试卷 题型:解答题
如图,一副三角饭的两个直角顶点重合在一起,
(1)比较大小:∠AOC__∠BOD,理由是__;
(2)∠AOD与∠BOC的和为多少度?为什么?

查看答案和解析>>
科目:初中数学 来源:2017年贵州省中考数学二模试卷 题型:单选题
下列命题正确的个数有( )
①相等的圆周角所对的弧相等;②圆的两条平行弦所夹的弧相等;③三点确定一个圆;④在同圆或等圆中,同弦或等弦所对的圆周角相等或互补.
A. 1 B. 2 C. 3 D. 4
B 【解析】根据与圆有关的基本概念依次分析即可. ①在同圆或等圆中,相等的圆周角所对的弧相等故错误;②圆中两条平行弦所夹的弧相等,正确;③不在同一直线上的三点确定一个圆,故错误;④在同圆或等圆中,同弦或等弦所对的圆周角相等或互补,正确. 故选B.查看答案和解析>>
科目:初中数学 来源:黄金30题系列 九年级数学 大题易丢分 题型:解答题
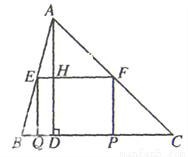
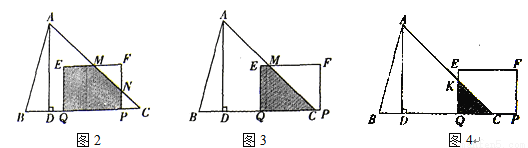
如图,在△ABC中,∠C=45°,BC=10,高AD=8,矩形EFPQ的一边QP在BC边上,E、F两点分别在AB、AC上,AD交EF于点H.
(1)求证: 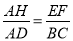 ;
;
(2)设EF=x,当x为何值时,矩形EFPQ的面积最大?并求其最大值;
(3)当矩形EFPQ的面积最大时,该矩形EFPQ以每秒1个单位的速度沿射线QC匀速运动(当点Q与点C重合时停止运动),设运动时间为t秒,矩形EFFQ与△ABC重叠部分的面积为S,求S与t的函数关系式.
【答案】(1)证明见解析;(2)当x=5时,S矩形EFPQ有最大值,最大值为20;(3)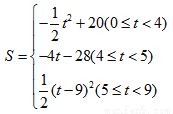
【解析】试题分析:(1)本题利用相似三角形的性质——相似三角形的对应边上的高之比等于相似比解决;(2)根据第一问的结论,即可根据矩形的面积公式得到关于矩形EFPQ的面积和x的函数关系式,根据函数的性质即可得到矩形的最大面积及对应的x的值;(3)此题要理清几个关键点,当矩形的面积最大时,由(2)可知此时EF=5,EQ=4;易证得△CPF是等腰Rt△,则PC=PF=4,QC=QP+PC=9;
一、P、C重合时,矩形移动的距离为PC(即4),运动的时间为4s;
二、E在线段AC上时,矩形移动的距离为9-4=5,运动的时间为5s;
三、Q、C重合时,矩形运动的距离为QC(即9),运动的时间为9s;
所以本题要分三种情况,分别写出解析式即可.
试题解析:
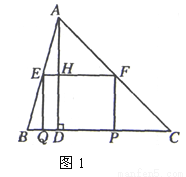
(1)∵ 四边形EFPQ是矩形,∴ EF∥QP.∴ △AEF∽△ABC.
又∵ AD⊥BC,
∴ AH⊥EF,∴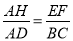
(2)由(1)得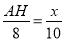 ,∴ AH=
,∴ AH=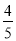 x.
x.
∴ EQ=HD=AD-AH=8-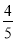 x,
x,
∴ S矩形EFPQ=EF·EQ=x (8-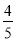 x) =-
x) =-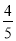 x2+8 x=-
x2+8 x=-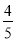 (x-5)2+20.
(x-5)2+20.
∵ -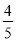 <0, ∴ 当x=5时,S矩形EFPQ有最大值,最大值为20.
<0, ∴ 当x=5时,S矩形EFPQ有最大值,最大值为20.
(3)如图1,由(2)
得EF=5,EQ=4.
∵∠C=45°,∴ △FPC是等腰直角三角形.
∴ PC=FP=EQ=4,QC=QP+PC=9.
分三种情况讨论:① 如图2.当0≤t<4时,
设EF、PF分别交AC于点M、N,则△MFN是等腰直角三角形,
∴ FN=MF=t.
∴S=S矩形EFPQ-SRt△MFN=20-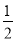 t2=-
t2=-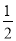 t2+20;
t2+20;
②如图3,当4≤t<5时,则ME=5-t,QC=9-t.
∴ S=S梯形EMCQ=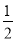 [(5-t)+(9-t )]×4=-4t+28;
[(5-t)+(9-t )]×4=-4t+28;
③如图4,当5≤t≤9时,设EQ交AC于点K,则KQ=QC=9-t.
∴ S=S△KQC=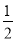 (9-t)2=
(9-t)2=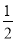 ( t-9)2.
( t-9)2.
综上所述:S与t的函数关系式为:
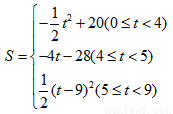
点睛:此题主要考查了矩形、等腰直角三角形的性质,相似三角形的判定和性质及二次函数的应用等知识,同时还考查了分类讨论的数学思想.
【题型】解答题
【结束】
12
已知关于x的一元二次方程x2-(2k+1)x+k2+2k=0有两个实数根x1,x2.
(1)求实数k的取值范围;
(2)是否存在实数k,使得x1·x2-x12-x22≥0成立?若存在,请求出k的值;若不存在,请说明理由.
(1)当k≤时,原方程有两个实数根(2)不存在实数k,使得x1·x2-x12-x22≥0成立 【解析】试题分析:(1)根据一元二次方程根的判别式列出不等式,解之即可;(2)本题利用韦达定理解决. 试题解析: (1) ,解得 (2)由 , 由根与系数的关系可得: 代入得: , 化简得: , 得. 由于的取值范围为, 故不存在k使。 ...查看答案和解析>>
科目:初中数学 来源:黄金30题系列 九年级数学 大题易丢分 题型:解答题
设a是方程x2﹣2006x+1=0的一个根,求代数式a2﹣2007a+ 的值.
的值.
【答案】-1
【解析】【试题分析】根据方程的根的定义,则x=a代入方程,可得:a2-2006a+1=0,
所以a2-2006a=-1,a2+1=2006a,得a2﹣2007a+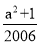 =
= .
.
【试题解析】
把x=a代入方程,可得:a2-2006a+1=0,
所以a2-2006a=-1,a2+1=2006a,
所以a2-2007a=-a-1,
所以a2-2007a+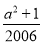 =-a-1+
=-a-1+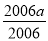 =-1,即a2-2007a+
=-1,即a2-2007a+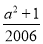 =-1.
=-1.
【方法点睛】本题目是一道考查一元二次方程的根的定义,方程的根满足该方程,代入得到相关代数式的值,进而将所求的额代数式进行转化,化简,求值.题目难度一般.
【题型】解答题
【结束】
5
如图,Rt△ABC中,∠BAC=60°,点O为Rt△ABC斜边AB上的一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD.
(1)求∠CAD的度数;
(2)若OA = 2,求阴影部分的面积(结果保留π).
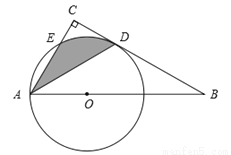
查看答案和解析>>
科目:初中数学 来源:黄金30题系列 七年级数学 小题易丢分 题型:填空题
某种数字化的信息传输中,先将信息转化为由数字 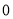 和
和 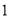 组成的数字串,并对数字串进行加密后再传输.现采用一种简单的加密方法:将原有的每个
组成的数字串,并对数字串进行加密后再传输.现采用一种简单的加密方法:将原有的每个  都变成
都变成 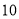 ,原有的每个
,原有的每个  都变成
都变成  .我们用
.我们用  表示没有经过加密的数字串.这样对
表示没有经过加密的数字串.这样对 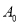 进行一次加密就得到一个新的数字串
进行一次加密就得到一个新的数字串  ,对
,对  再进行一次加密又得到一个新的数字串
再进行一次加密又得到一个新的数字串 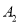 ,依此类推,
,依此类推,  .例如
.例如  :
:  ,则
,则 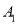 :
:  .若已知
.若已知 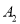 :
:  ,则
,则 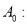 ________________;若数字串
________________;若数字串 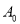 共有
共有 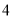 个数字,则数字串
个数字,则数字串 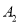 中相邻两个数字相等的数对至少有________________对.
中相邻两个数字相等的数对至少有________________对.
查看答案和解析>>
科目:初中数学 来源:黄金30题系列 七年级数学 小题易丢分 题型:填空题
若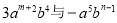 的和仍是一个单项式,则
的和仍是一个单项式,则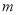 +
+ 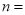 _____________________
_____________________
查看答案和解析>>
科目:初中数学 来源:黄金30题系列 七年级数学 小题易丢分 题型:单选题
方程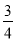 [
[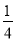 (x+1)+4]=3
(x+1)+4]=3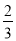 +
+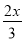 变形第一步较好的方法是( )
变形第一步较好的方法是( )
A. 去分母 B. 去括号 C. 移项 D. 合并同类项
A 【解析】试题解析:根据题意可得:先去分母比较简单,因为去分母后,去括号、移项时系数都变为整数,计算变得比较简单. 故选A.查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级北师大版数学试卷(B卷) 题型:填空题
如图,用4个相同的直角三角形与一个小正方形拼成的大正方形,若图中直角三角形较短的直角边长是5㎝,小正方形的边长是7㎝,则大正方形的边长是_______㎝。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com