
勾股定理是几何中的一个重要定理.在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的,∠BAC=90°,AB=3,AC=4,点D,E,F,G,H,I都在矩形KLMJ的边上,则矩形KLMJ的面积为( )
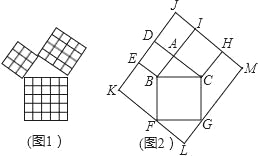
A. 90 B. 100 C. 110 D. 121
C 【解析】试题解析:如图,延长AB交KF于点O,延长AC交GM于点P, 所以四边形AOLP是正方形, 边长AO=AB+AC=3+4=7, 所以KL=3+7=10,LM=4+7=11, 因此矩形KLMJ的面积为10×11=110. 故选C.科目:初中数学 来源:北京市西城外国语学校2017-2018学年度第一学期八年级数学期中试卷 题型:填空题
已知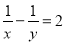 ,则分式
,则分式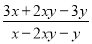 的值等于__________.
的值等于__________.
查看答案和解析>>
科目:初中数学 来源:黑龙江省大庆市2016---2017学年度上期初三数学期末试卷 题型:填空题
如果不等式组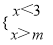 无解,那么m的取值范围是 ______ .
无解,那么m的取值范围是 ______ .
查看答案和解析>>
科目:初中数学 来源:浙江省余姚市2017-2018学年八年级上学期期中考试数学试卷 题型:解答题
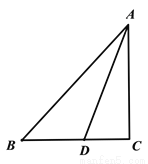
如图所示,已知:Rt△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线.
求证:AC+CD=AB.
查看答案和解析>>
科目:初中数学 来源:浙江省余姚市2017-2018学年八年级上学期期中考试数学试卷 题型:解答题
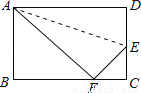
如图,折叠矩形的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,求EC的长.
查看答案和解析>>
科目:初中数学 来源:浙江省余姚市2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
等腰三角形有两条边的长为4cm和9cm,则该三角形的周长( )
A. 17cm B. 22cm C. 17cm和22cm D. 18cm
B 【解析】试题分析:当4为底时,则三角形的周长为:4+9+9=22cm;当9为底时,4、4、9不能构成三角形.查看答案和解析>>
科目:初中数学 来源:南京市玄武区2016~2017学年度第一学期期九年级试卷 题型:解答题
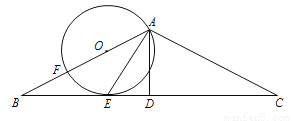
如图,在△ABC中,AB=AC,AD为△ABC的中线,O为AB上一点,以O为圆心,AO为半径的⊙O与AB交于点F,与BC交于点E.连接AE,AE平分∠BAD.
(1)求证:BC与⊙O相切于点E;
(2)若AB=10,BC=16,求⊙O的半径;
(3)若AD与⊙O的交点为△ABC的重心,则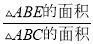 的值为 .
的值为 .
查看答案和解析>>
科目:初中数学 来源:南京市玄武区2016~2017学年度第一学期期九年级试卷 题型:填空题
已知P是线段AB的黄金分割点,AP>PB,AB=2,则AP=__________.
-1 【解析】由于P为线段AB=2的黄金分割点, 且AP是较长线段; 则AP=2×.故答案为: .查看答案和解析>>
科目:初中数学 来源:广东省揭阳市揭西县2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
计算: 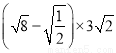
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com