
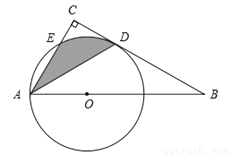
��ͼ��Rt��ABC�У���BAC=60�㣬��OΪRt��ABCб��AB�ϵ�һ�㣬��OAΪ�뾶�ġ�O��BC���ڵ�D����AC���ڵ�E������AD.
��1�����CAD�Ķ�����
��2����OA = 2������Ӱ���ֵ��������������У�.
���𰸡���1����CAD�Ķ���Ϊ30�㣻
��2����Ӱ���ֵ����Ϊ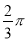 .
.
�������������������1������OD�������ߵ����ʿ�֪OD��BC���Ӷ���֤��AC��OD����ƽ���ߵ����ʺ͵��������ε����ʿ�֤����CAD=��OAD����2������OE��ED��OD����֤��ED��AO��Ȼ������ͬ�ȸߵ����������ε������ȿ�֪S��AED=S��EDO�����ǽ���Ӱ���ֵ������ת��Ϊ����EOD�������⼴�ɣ�
�����������1������OD��
��BC�ǡ�O�����ߣ�DΪ�е㣬
��OD��BC.
�֡�AC��BC��
��OD��AC��
���ADO=��CAD.
�֡�OD=OA��
���ADO=��OAD��
���CAD=��OAD=30��.
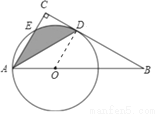
��2������OE��ED.
�ߡ�BAC=60�㣬OE=OA��
���OAEΪ�ȱ������Σ�
���AOE=60�㣬
���ADE=30��.
�֡�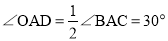 ��
��
���ADE=��OAD��
��ED��AO��
��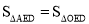
����Ӱ���ֵ���� = 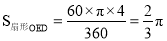 .
.
�����͡������
��������
6
��ͼ����������������϶��ɵ�һ������ͼ�ε�����ͼ������ͼ������ߴ磨��λ��mm�������������ͼ�εı������
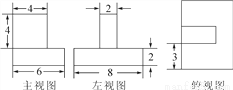
 �п�������㾫��ϵ�д�
�п�������㾫��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ�����а�����2017-2018ѧ����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ���ѡ��
��֪����������y����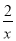 ����x��0ʱ������ͼ����( )
����x��0ʱ������ͼ����( )
A. ��һ���� B. �ڶ����� C. �������� D. ��������
D ���������߱���ϵ��k=?2<0������ͼ��λ�ڶ��������ޣ� ��x>0���෴����������ͼ��λ�ڵ������ޣ� ��ѡ��D.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʡ�п���ѧ��ģ�Ծ� ���ͣ������
��ͼ��ABΪԲO��ֱ������CD��AB������Ϊ��E������OC����OC=5��CD=8����AE=_____��
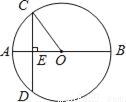
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���ƽ�30��ϵ�� ���꼶��ѧ �������� ���ͣ������
ij�̼Ҿ���һ���̲裬����װ��������Ͷ��3000Ԫ����֪�̲�ÿǧ�˳ɱ�50Ԫ�����о���������y��kg�������۵���x��Ԫ/ kg���ı仯���仯������仯�������±���ʾ��

����̲������������Ϊw��Ԫ�������������ۡ����������ɱ���
��1��������ϱ������y��x֮��ĺ�����ϵʽ������д���Ա���x��ȡֵ��Χ����
��2����w��x֮��ĺ�����ϵʽ������д���Ա���x��ȡֵ��Χ���������xΪ��ֵʱ��w��ֵ���
��3�����ڵ�һ�������ʹw������ֵ�����۵��۽������ۺ��ڵڶ�����������۲��Ÿ�Ԥ�����۵��۲��ø���80Ԫ��Ҫ����ȫ���ջ�װ��Ͷ�ʵĻ�����ʹ�ڶ����µ��������ٴﵽ1700Ԫ����ô�ڶ�����ʱ��Ӧ��ȷ�����۵�����ʲô��Χ�ڣ�
���𰸡���1��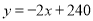 ��
��
��2��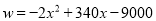 ����
����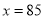 ʱ��
ʱ�� 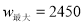 ��
��
��3�������۵���Ϊ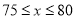 Ԫʱ����ȫ���ջ�Ͷ�ʵĻ�����ʹ�ڶ����µ�������1700Ԫ.
Ԫʱ����ȫ���ջ�Ͷ�ʵĻ�����ʹ�ڶ����µ�������1700Ԫ.
���������������������1�����ݱ��������.�����۵���ÿ����5Ԫ���������½�10Kg����w��x��һ�κ�����������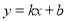 ������70��100������75��90��������ʽ�ã�
������70��100������75��90��������ʽ�ã�
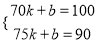 ��ã�
��ã� 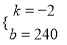 ����
����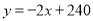 ��
��
��2����������=������������������������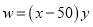
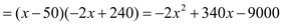 ����Ϊ����ʽ�ã�
����Ϊ����ʽ�ã� 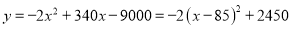 ����
����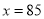 ʱ��
ʱ�� 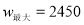
��3���ɣ�2��֪����1���»���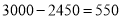 Ԫ��Ͷ�ʳɱ�û���ջأ���Ҫ����ȫ����Ͷ�ʵĻ�����ʹ�ڶ����µ�����ﵽ1700Ԫ�� ��
Ԫ��Ͷ�ʳɱ�û���ջأ���Ҫ����ȫ����Ͷ�ʵĻ�����ʹ�ڶ����µ�����ﵽ1700Ԫ�� ��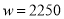 �ſ��ԣ��ɵ÷���
�ſ��ԣ��ɵ÷���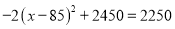 ����ã�
����ã� 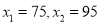 ��������
��������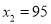 �������⣬Ӧ��ȥ.��
�������⣬Ӧ��ȥ.��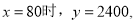 ����Ϊ-2<0���������߿������£���
����Ϊ-2<0���������߿������£���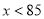 ʱ��
ʱ�� 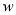 ��
��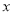 �����������
�����������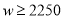 �������۵��۲�����80ʱ��
�������۵��۲�����80ʱ�� 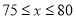
�����������
��1����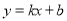 ������70��100������75��90��������ʽ�ã�
������70��100������75��90��������ʽ�ã�
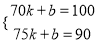 ��ã�
��ã� 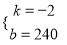 ����
����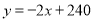 ��
��
������������Ӧֵ������ʽ������������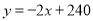
��2��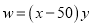
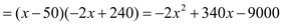
��ˣ� 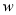 ��
��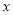 �Ĺ�ϵʽΪ
�Ĺ�ϵʽΪ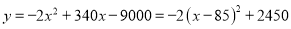
��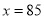 ʱ��
ʱ�� 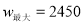
��3���ɣ�2��֪����1���»���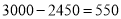 Ԫ��Ͷ�ʳɱ�û���ջأ�
Ԫ��Ͷ�ʳɱ�û���ջأ�
��Ҫ����ȫ����Ͷ�ʵĻ�����ʹ�ڶ����µ�����ﵽ1700Ԫ�� ��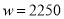 �ſ��ԣ�
�ſ��ԣ�
�ɵ÷���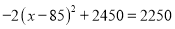 ����ã�
����ã� 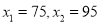
��������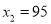 �������⣬Ӧ��ȥ.��
�������⣬Ӧ��ȥ.��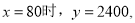 ��
��
��-2<0���࣬��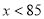 ʱ��
ʱ�� 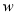 ��
��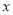 �����������
�����������
��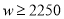 �������۵��۲�����80ʱ��
�������۵��۲�����80ʱ�� 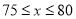
�𣺵����۵���Ϊ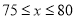 Ԫʱ����ȫ���ջ�Ͷ�ʵĻ�����ʹ�ڶ����µ�������1700Ԫ
Ԫʱ����ȫ���ջ�Ͷ�ʵĻ�����ʹ�ڶ����µ�������1700Ԫ
�����͡������
��������
18
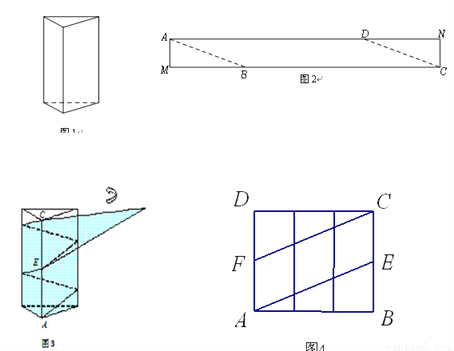
��ͼ���ֱ��ǿɻ�����κ�ƽ���ı���ѧ�ߣ���֪ƽ���ı��ν϶̵ı������εı߳���ȣ�
��1����һ����ѧ��У�ijС��ѧ�������ε�һ����ƽ���ı��ν϶̱��غϣ���ƴ����ͼ1��ʾ��ͼ�Σ�AF������C������DE��AF�ڵ�M���۲췢�֣���M��DE���е㣮
��������λѧ���д����Ե�֤��˼·��
˼·1�������������ߣ�ֱ��֤������ȫ�ȣ�
˼·2����֤������ȫ�ȣ�����BD��AF�ڵ�H����
��ο������˼·��֤����M��DE���е㣨ֻ����һ�ַ���֤������
��2����ͼ2���ڣ�1����ǰ���£�����ABE=135��ʱ���ӳ�AD��EF���ڵ�N����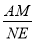 ��ֵ��
��ֵ��
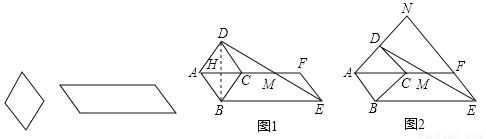
��3���ڣ�2���������£��� =k��kΪ����
=k��kΪ���� �ij�������ֱ���ú�k�Ĵ���ʽ��ʾ
�ij�������ֱ���ú�k�Ĵ���ʽ��ʾ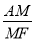 ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���ƽ�30��ϵ�� ���꼶��ѧ �������� ���ͣ������
��ͼ1��һ����������װ�У����ĵ����DZ߳�Ϊ10cm���������Σ��������涼�Ǿ��Σ��ֽ���Ϊ15cm�IJ�ɫ����ֽ��AMCN�ü���һ��ƽ���ı���ABCD����ͼ2����Ȼ��������ƽ���ı���ֽ������ͼ3�ķ�ʽ�������������װ�еIJ�����а�����Ҫ�����ʱû���ص����֣���ֽ���ڲ��������Ȧ�����ý������������װ�еIJ���ȫ������������ͼ3�У����������ع���A�IJ���������õ���ͼ4�IJ���չ��ͼ.Ϊ�˵õ��ü��ĽǶ�,���ǿ��Ը���չ��ͼƴ�ӳ�����������ƽ���ı��ν����о�.
��1������ͼ4�л���ƴ�Ӻ����������ƽ���ı��Σ�
��2������ͼ2�У�����ü��ĽǶȣ�����ABM�Ķ�����.
���𰸡���1����ͼ����������2����ABM=30�㣮
����������������1����ͼ4�еġ�ABE����ƽ��30cm����CDF����ƽ��30cm��ƴ����ͼ�е�ƽ���ı��Σ���ƽ���ı��μ�Ϊͼ2�е��ı���ABCD��
��2���������������AB=30cm����ֽ���Ŀ�Ϊ15cm���������Ǻ�����á�AMB=30�㣮
�����������1����ͼ��
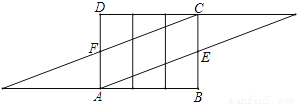
��2����ͼ2�İ�������֪��AB�ij������������ĵױ��ܳ�����AB=30��
�� ֽ����Ϊ15���� sin��ABM =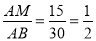 �����AMB=30�㣮
�����AMB=30�㣮
�����͡������
��������
11
��ͼ���ڡ�ABC�У���C��45�㣬BC��10����AD��8������EFPQ��һ��QP��BC���ϣ�E��F����ֱ���AB��AC�ϣ�AD��EF�ڵ�H��
��1����֤�� 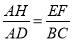 ��
��
��2����EF��x����xΪ��ֵʱ������EFPQ���������������ֵ��
��3��������EFPQ��������ʱ���þ���EFPQ��ÿ��1����λ���ٶ�������QC�����˶�������Q���C�غ�ʱֹͣ�˶��������˶�ʱ��Ϊt�룬����EFFQ���ABC�ص����ֵ����ΪS����S��t�ĺ�����ϵʽ��
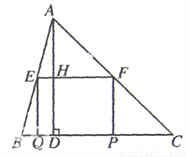
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���ƽ�30��ϵ�� ���꼶��ѧ �������� ���ͣ������
��ͼ��һ�κ���y=kx+b�뷴��������y= ��ͼ����A��1��6����B��3��n�����㣮
��ͼ����A��1��6����B��3��n�����㣮
��1������������һ�κ����ı���ʽ��
��2������ͼ��д������ʽkx+b��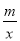 ��0�Ľ⼯��
��0�Ľ⼯��
��3������M��x���ϡ���N��y���ϣ�����M��N��A��BΪ������ı�����ƽ���ı��Σ���ֱ��д����M��N�����꣮
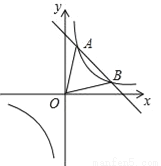
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���ƽ�30��ϵ�� ���꼶��ѧ С������ ���ͣ������
С����Χ�����ų�����һ���й��ɵ�ͼ�������е�1��ͼ����1ö���ӣ���2��ͼ����3ö���ӣ���3��ͼ����4ö���ӣ���4��ͼ����6ö���ӣ�������ô��9��ͼ������������___ö��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���ƽ�30��ϵ�� ���꼶��ѧ С������ ���ͣ���ѡ��
����OC�ڡ�A0B�ڲ������������в���ȷ��OC�ǡ�AOB�Ľ�ƽ���ߵ��ǣ� ��
A. ��A0C=��BOC B. ��AOC+��BOC=��AOB C. ��AOB= 2��A0C D. ��BOC=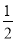 ��AOB
��AOB
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ���һѧ����ĩ��ϰ����֮����ϰģ������꼶��ʦ�����ѧ�Ծ���B���� ���ͣ������
���㣺
��1��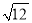 ��
��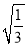 +
+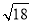 (2)
(2) 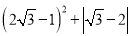
��3��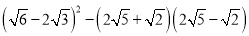 . ��4����-2��3+
. ��4����-2��3+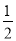 ��2004-
��2004-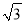 ��0-|-
��0-|-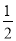 |
|
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com