
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源:北师大版数学七年级下册第三章3.2用关系式表示的变量间关系课时练习 题型:单选题
汽车离开甲站10千米后,以60千米/时的速度匀速前进了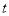 小时,则汽车离开甲站所走的路程
小时,则汽车离开甲站所走的路程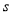 (千米)与时间
(千米)与时间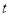 (小时)之间的关系式是( )
(小时)之间的关系式是( )
A. 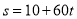 B.
B. 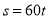 C.
C. 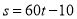 D.
D. 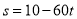
查看答案和解析>>
科目:初中数学 来源:北师大版七年级下册 第三章 变量之间的关系 3.1 用表格表示的变量间关系 同步练习 题型:解答题
星期天小明和同学们去郊外爬山,得到如下数据:
爬坡长度x(米) | 40 | 80 | 120 | 160 | 200 | 240 |
爬坡时间t(分) | 2 | 5 | 9 | 14 | 20 | 30 |
(1)当爬到120米时,所用时间是多少?
(2)爬坡速度随时间是怎样变化的?
(1)9分钟; (2)爬坡速度随时间的增加而减小. 【解析】试题分析:(1)观察表格信息可知爬坡120m时,所需时间为9分钟 (2)计算爬坡相同的距离所用的时间,即可得出结论. 试题解析:(1)观察表格信息可知爬坡120m时,所需时间为9分钟 (2)由图表可知爬坡长度分别为40m和80m时,所用时间分别为2分钟和5分钟 故此时爬坡每增加10m时,所需时间为分钟 ...查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下2.2.2 用“内错角、同旁内角”判定平行线 同步练习 题型:解答题
如图,∠1=65°,∠2=65°,∠3=115°.试说明:DE∥BC,DF∥AB.根据图形,完成下面的推理:
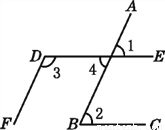
因为∠1=65°,∠2=65°,
所以∠1=∠2.
所以______________∥ ( ).
因为AB与DE相交,
所以∠1=∠4( ).
所以∠4=65°.
又因为∠3=115°,
所以∠3+∠4=180°.
所以 ∥ ( ).
 DE;BC;同位角相等,两直线平行;对顶角相等;DF;AB;同旁内角互补,两直线平行
【解析】试题分析:由同位角相等,两直线平行可得DE∥BC,由对顶角相等可得∠4=65°,再由同旁内角互补,两直线平行可得DF∥AB.
试题解析:因为∠1=65°,∠2=65°,
所以∠1=∠2.
所以DE∥BC (同位角相等,两直线平行).
因为AB与DE相交,
所以∠1=∠...
DE;BC;同位角相等,两直线平行;对顶角相等;DF;AB;同旁内角互补,两直线平行
【解析】试题分析:由同位角相等,两直线平行可得DE∥BC,由对顶角相等可得∠4=65°,再由同旁内角互补,两直线平行可得DF∥AB.
试题解析:因为∠1=65°,∠2=65°,
所以∠1=∠2.
所以DE∥BC (同位角相等,两直线平行).
因为AB与DE相交,
所以∠1=∠...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com