
如果把一个锐角三角形三边的长都扩大为原来的两倍,那么锐角A的余切值
A. 扩大为原来的两倍; B. 缩小为原来的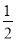 ;
;
C. 不变; D. 不能确定.
C 【解析】因为△ABC三边的长度都扩大为原来的2倍所得的三角形与原三角形相似, 所以锐角A的大小没改变,所以锐角A的余切值也不变. 故选:C. 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源:北京市平谷区2018届初三第一学期期末数学试卷 题型:解答题
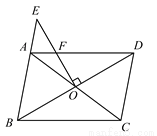
如图,在□ABCD中,对角线AC,BD交于点O,过点O作EO⊥BD,交BA延长线于点E,交AD于点F,若EF=OF,∠CBD=30°,BD=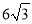 .求AF的长.
.求AF的长.
查看答案和解析>>
科目:初中数学 来源:安徽省六安市2018届九年级上学期第二次月考数学试卷 题型:单选题
如图,PA,PB是⊙O的两条切线,切点是A,B.如果OP=4,OA=2,那么∠AOB=( )

A. 90° B. 100° C. 120° D. 150°
C 【解析】由切线长定理知△APO≌△BPO,得∠AOP=∠BOP.可求得cos∠AOP=2:4=,所以可知∠AOP=60°,从而求得∠AOB=120°. 故选:C.查看答案和解析>>
科目:初中数学 来源:上海浦东新区2017-2018学年九年级上学期期末数学试卷(初三一模) 题型:填空题
将抛物线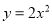 向下平移3个单位,所得的抛物线的表达式是 .
向下平移3个单位,所得的抛物线的表达式是 .
查看答案和解析>>
科目:初中数学 来源:上海浦东新区2017-2018学年九年级上学期期末数学试卷(初三一模) 题型:单选题
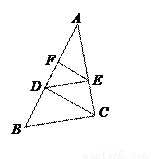
如图,已知点D、F在△ABC的边AB上,点E在边AC上,且DE∥BC,要使得EF∥CD,还需添加一个条件,这个条件可以是
A. 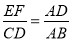 ; B.
; B. 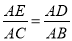 ;
;
C. 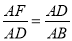 ; D.
; D. 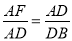 .
.
查看答案和解析>>
科目:初中数学 来源:云南省2018届九年级上学期期中考试数学试卷 题型:解答题
已知关于x的一元二次方程为:x2+2x+2k-4=0.
(1)当方程有两实数根时,求k的取值范围;
(2)任取一个k值,求出方程的两个不相等实数根.
(1)k≤;(2) , . 【解析】(1)根据一元二次方程的根的判别式,建立关于k的不等式,求出k的取值范围; (2)先确定k=1或2,再根据方程的根都是整数,可知20-8k是完全平方数,即可求k的值. 【解析】 (1)关于x的一元二次方程x2+2x+2k-4=0中, ∴a=1,b=2,c=2k-4, ∵方程有两个不相等的实数根, ∴△=b2-4ac=20-8k>0, ∴k...查看答案和解析>>
科目:初中数学 来源:云南省2018届九年级上学期期中考试数学试卷 题型:填空题
一条排水管的截面如图所示,已知排水管的半径OA=1m,水面宽AB=1.2m,某天下雨后,水管水面上升了0.2m,则此时排水管水面宽CD等于_________m.
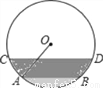
查看答案和解析>>
科目:初中数学 来源:2017-2018学年度第一学期海南省海口市九年级数学科期末检测题 题型:填空题
如图,某村准备在坡度为i =1: 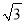 的斜坡上栽树,要求相邻两棵树之间的水平距离为5米,则这两棵树在坡面上的距离AB为____________米.(结果保留根号)
的斜坡上栽树,要求相邻两棵树之间的水平距离为5米,则这两棵树在坡面上的距离AB为____________米.(结果保留根号)
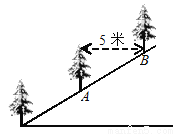
查看答案和解析>>
科目:初中数学 来源:内蒙古赤峰市宁城县2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
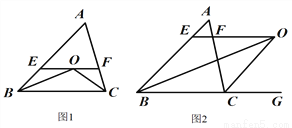
已知,如图1:△ABC中,∠B、∠C的平分线相交于点O,过点O作EF∥BC交AB、AC于E、F.
(1)直接写出图1中所有的等腰三角形,并指出EF与BE、CF间有怎样的数量关系?
(2)在(1)的条件下,若AB=10,AC=15,求△AEF的周长.
(3)如图2,若△ABC中,∠B的平分线与三角形外角∠ACG的平分线CO交于点O,过O点作OE∥BC交AB于E,交AC于F,请问(1)中EF与BE、CF间的关系还是否存在,若存在,说明理由;若不存在,写出三者新的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com