
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源:2017年天津109中中考数学模拟试卷 题型:单选题
计算5-(-2)×3的结果等于( )
A. -11 B. -1 C. 1 D. 11
D 【解析】5-(-2)×3 故选D.查看答案和解析>>
科目:初中数学 来源:浙江省杭州市2018届九年级上学期期中考试数学试卷(含解析) 题型:单选题
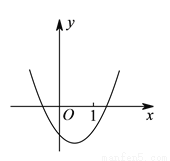
“已知二次函数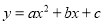 的图像如图所示,试判断
的图像如图所示,试判断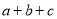 与
与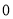 的大小.”一同学是这样回答的:“由图像可知:当
的大小.”一同学是这样回答的:“由图像可知:当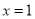 时
时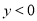 ,所以
,所以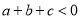 .”他这种说明问题的方式体现的数学思想方法叫做( ).
.”他这种说明问题的方式体现的数学思想方法叫做( ).
A. 换元法 B. 配方法 C. 数形结合法 D. 分类讨论法
C 【解析】试题解析:由解析式可推出,x=1时y=a+b+c; 然后结合图象可以看出x=1时对应y的值小于0,所以可得a+b+c<0. 解决此题时将解析式与图象紧密结合,所以解决此题利用的数学思想方法叫做数形结合法. 故选C.查看答案和解析>>
科目:初中数学 来源:江苏省无锡市2017-2018学年七年级12月月考数学试卷 题型:填空题
如果单项式﹣x3ym﹣2与x3y的差仍然是一个单项式,则m=____.
3 【解析】试题分析:∵单项式-x3ym-2与x3y的差仍然是一个单项式, ∴m-2=1, 解得:m=3. 故答案为:3.查看答案和解析>>
科目:初中数学 来源:江苏省无锡市2017-2018学年七年级12月月考数学试卷 题型:单选题
如图,把左边的图形绕着给定的直线旋转一周后形成的几何体是( )

A.  B.
B. 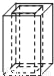 C.
C. 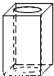 D.
D. 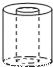
查看答案和解析>>
科目:初中数学 来源:2017年河北省中考数学模拟试卷 题型:解答题
如图,在△ABC中,AC=DC=DB,∠ACD=100°,求∠B的度数.
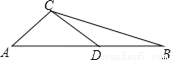
查看答案和解析>>
科目:初中数学 来源:2017年河北省中考数学模拟试卷 题型:单选题
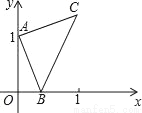
如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰Rt△ABC,使∠BAC=90°,设点B的横坐标为x,设点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )
A. 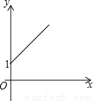 B.
B. 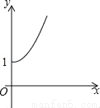 C.
C. 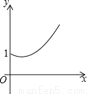 D.
D. 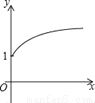
查看答案和解析>>
科目:初中数学 来源:2017年陕西师大附中中考数学二模试卷 题型:解答题
为了提高足球基本功,甲、乙、丙三位同学进行足球传球训练,球从一个人脚下随机传到另一个人脚下,且每位传球人传球给其余两人的机会是均等的,由甲开始传球,共传三次.
(1)请用树状图列举出三次传球的所有可能情况;
(2)三次传球后,球回到甲脚下的概率大还是传到乙脚下的概率大?
(1)、答案见解析;(2)、球回到乙脚下的概率大 【解析】 试题分析:(1)、根据题意画出树状图即可;(2)、根据(1)的树形图,利用概率公式列式进行计算即可得解,分别求出球回到甲脚下的概率和传到乙脚下的概率,比较大小即可. 试题解析:(1)、根据题意画出树状图如下: 由树形图可知三次传球有8种等可能结果; (2)、由(1)可知三次传球后,球回到甲脚下的概率==;传到...查看答案和解析>>
科目:初中数学 来源:广东省深圳市2017-2018北师大版八年级(上)数学期末模拟试卷 题型:单选题
如图,在长方形ABCD中,点E在AB边上,将长方形ABCD沿直线DE折叠,点A恰好落在BC边上的点F处.若AE=5,BF=3,则CF的长为( )
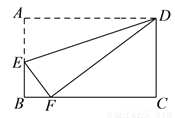
A. 9 B. 10 C. 12 D. 15
C 【解析】∵四边形ABCD是长方形, ∴∠B=∠C=∠A=90°,AB=CD, 由折叠的性质可得:EF=AE=5,∠EFD=∠A=90°, 在Rt△BEF中,BE==4,∠BFE+∠BEF=90°, ∴CD=AB=AE+BE=5+4=9, ∵∠EFD=90°,∴∠BFE+∠DFC=90°, ∴∠BEF=∠CFD, ∴△BEF∽△CFD, ∴,...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com